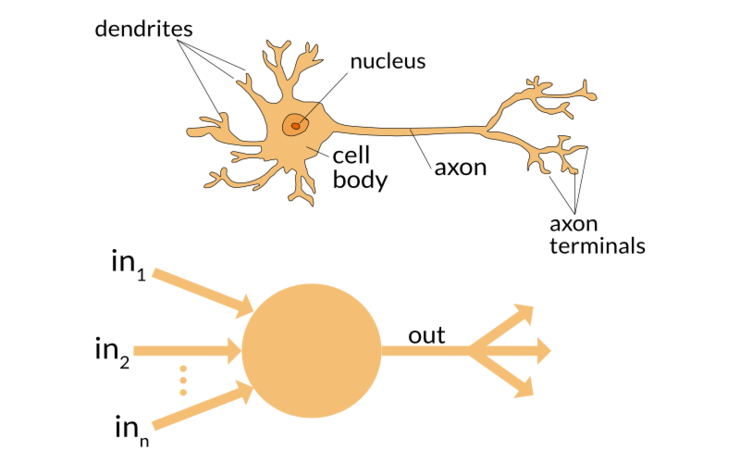
이번 포스팅에서는 [3편]에서 보인 퍼셉트론을 파이썬으로 구현한 perceptron.py 코드에 대해 설명을 합니다.
perceptron.py
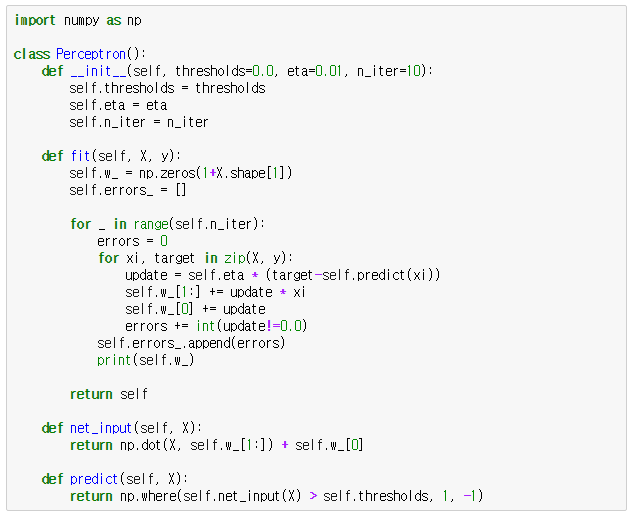
>>> import numpy as np
numpy 모듈을 임포트합니다.
>>> class Perceptron()
퍼셉트론을 구현하는 클래스를 정의하고, 주요 알고리즘은 클래스 멤버 함수로 구현할 것입니다.
>>> def __init__(self, thresholds=0.0, eta=0.01, n_iter=10)
Perceptron 클래스의 생성자를 정의합니다. 생성자의 기본인자로 임계값, learning rate, 학습 횟수를 지정하는 thresholds, eta, n_iter의 디폴트 값을 각각 0.0, 0.01, 10으로 지정하고 있습니다.
>>> def fit(self, X, y)
트레이닝 데이터 X와 실제 결과값 y를 인자로 받아 머신러닝을 수행하는 함수입니다. 머신러닝 분야에서 일반적으로 트레이닝 데이터를 대문자 X로, 실제 결과값을 소문자 y로 표현합니다. 여기서도 이 관습을 따라 X, y를 각각 트레이닝 데이터, 실제 결과값을 의미하는 인자로 정의한 겁니다.
>>> self.w_ = np.zeros(1+X.shape[1])
가중치를 numpy 배열로 정의합니다. X.shape[1]은 트레이닝 데이터의 입력값 개수를 의미합니다. 예를 들어 X가 4 x 2 배열인 경우, X.shape의 값은 (4, 2)가 되며 X.shape[1]의 값은 2가 됩니다. 이 경우 self.w_는 np.zeros(3)이 될 것이고, 실제 값은 numpy 배열 [0. 0. 0.]이 됩니다.
>>> self.errors_ = []
머신러닝 반복 회수에 따라 퍼셉트론의 예측값과 실제 결과값이 다른 오류 회수를 저장하기 위한 변수입니다.
>>> for _ in range(self.n_iter):
errors = 0
for xi, target in zip(X, y):
update = self.eta * (target - self.predict(xi))
self.w_[1:] += update * xi
self.w_[0] += update
errors += int(update != 0.0)
self.errors_.append(errors)
print(self.w_)
self.n_iter로 지정한 숫자만큼 반복합니다. for 다음에 적힌 _은 아무런 의미가 없는 변수이며 단순히 for문을 특정 회수만큼 반복만 하고자 할 때 관습적으로 사용하는 변수라고 생각하면 됩니다.
초기 오류 횟수를 0으로 정의하고, 트레이닝 데이터 세트 X와 결과값 y를 하나씩 꺼집어내서 xi, target 변수에 대입합니다. xi는 하나의 트레이닝 데이터의 모든 입력값 x1~xn 을 의미합니다. 참고로 x0는 1로 정해져 있습니다.
update는 아래의 식에 대한 값입니다.
여기서 실제 결과값과 예측값에 대한 활성 함수 리턴값이 같게 되면 update는 0이 됩니다. 따라서 트레이닝 데이터 xi의 값에 곱해지는 가중치에 update * xi의 값을 단순하게 더함으로써 가중치를 업데이트 할 수 있는데, 이는 결과값과 예측값의 활성 함수 리턴값이 같아질 경우 0을 더하는 꼴이라 가중치의 변화가 없을 것이고, 결과값과 예측값의 활성 함수 리턴값이 다를 경우 0이 아닌 유효한 값이 더해져서 가중치가 업데이트 될 것이기 때문입니다. 마찬가지로 w0의 값에 해당하는 self.w_[0]에는 x0가 1이므로 update만 단순하게 더하면 됩니다. 여기까지가 아래의 식을 계산한 것이 됩니다.
update의 값이 0이 아닌 경우, errors의 값을 1증가시키고 다음 트레이닝 데이터로 넘어갑니다. 모든 트레이닝 데이터에 대해 1회 학습이 끝나면 self.errors_에 발생한 오류 횟수를 추가한 후, 가중치를 화면에 출력하고 다음 학습을 또 다시 반복합니다.
>>> def net_input(self, X):
return np.dot(X, self.w_[1:]) + self.w_[0]
numpy.dot(x, y)는 벡터 x, y의 내적 또는 행렬 x, y의 곱을 리턴합니다. 따라서 net_input(self, X)는 트레이닝 데이터 X의 각 입력값과 그에 따른 가중치를 곱한 총합, 즉 이전 포스팅에서 설명한 아래의 순입력 함수 결과값을 구현한 것입니다.
여기서 잠깐!
앞으로 이어질 머신러닝과 딥러닝에 대한 수식을 연산하거나 설명할 때 가장 많이 등장하는 개념이 벡터나 행렬입니다. 우리는 벡터와 행렬에 대해 고등학교 수학에서 배웠습니다. 그리고 이공계 대학을 나왔다면 선형대수학이라는 과목에서 관련된 내용을 모두 배웠으리라 생각합니다. 물론 이 포스팅을 읽고 있는 많은 분들이 벡터나 행렬, 선형대수학에 익숙하지 않은 사람들도 있겠지요~
그래서, 행렬에 대해 간단하게 짚고 넘어가도록 하겠습니다.
행렬이란 수들의 집합을 행과 열방향으로 나열해 놓은 것을 말합니다. 아래는 숫자 1, 2, 3, 4를 이용한 행렬의 한 예시를 보인 것입니다.
여기서 1, 2나 3, 4가 나열된 방향을 행이라 하고, 1, 3이나 2, 4가 나열된 방향을 열이라 합니다.
따라서 위에서 보인 행렬은 행이 2개, 열이 2개인 행렬이며, 이를 간단히 행과 열의 개수를 순서대로 적어 2 x 2(차원) 행렬이라 부릅니다. 만약 어떤 행렬 A가 행의 개수가 m개이고 열의 개수가 n개인 m x n 행렬이라면 다음과 같이 표현할 수 있습니다.
여기서, a11, a12 등을 행렬 A의 성분이라 부릅니다.
행렬이 어떤 것인지에 대해 대충 이해가 되었다면, 이제 행렬간 연산에 대해 알아봅니다. 행렬에서 가장 많이 사용되는 연산은 +, -, x 입니다.
먼저, 행렬 A, B가 있다고 할 때 두 행렬간 덧셈과 뺄셈이 가능하려면 두 행렬의 차원이 동일해야 합니다. A가 2 x 2행렬이면, B도 2 x 2 행렬이어야 더하기 또는 빼기가 가능하다는 것입니다.
행렬의 덧셈과 뺄셈은 두 행렬에서 일치하는 성분끼리 더하거나 빼면 됩니다. 행렬 A, B가 아래와 같다고 하고,
두 행렬 A, B의 덧셈은 다음과 같습니다.
행렬의 뺄셈도 마찬가지로 하면 되고요,~ 뭐, 다 아는 내용이니까 복습하는겸 해서 가볍게 보면 됩니다.
이제는 두 행렬의 곱셈에 대해서 살펴봅니다. 행렬간 곱셈은 더하기 빼기와는 좀 다르게 동작합니다. 행렬 A, B가 있다고 하고, 이 두 행렬의 곱 AB가 가능하려면 A와 B의 차원에 관계없이 A의 열의 개수와 B의 행의 개수가 동일하면 됩니다.
위의 두 행렬 A, B를 보면, A의 열의 개수와 B의 행의 개수가 n개로 동일하므로 A와 B의 곱 AB는 가능합니다. 하지만 B의 열의 개수와 A의 행의 개수는 다르므로 두 행렬의 곱 BA는 가능하지 않습니다. 이점 유의하세요~~
두 행렬의 곱이 가능한 조건이 충족되면 AB는 다음과 같이 정의 됩니다.
아,, 이거 간단한 수식으로 표현하려다 보니 복잡해보이네요.. 아래 그림을 보시죠..(말로 설명하면 쉽게 될걸 글로 하면 이렇게 어렵습니다..)
A의 1행과 B의 1열을 선택하고 A의 1행에 있는 성분과 B의 1열에 있는 성분끼리 곱하여 모두 더한 값을 결과 행렬의 (1, 1) 성분으로 합니다. 마찬가지로 A의 1행과 B의 2열을 성분끼리 곱한 후 모두 더한 값을 결과 행렬의 (1, 2) 성분으로 합니다. 이런 식으로 A의 모든 행과 B의 모든 열을 곱하여 결과 행렬의 해당되는 자리에 대입하면 됩니다.
따라서 A와 B의 곱 AB는 m x k 행렬이 됩니다.
이제, [3편] 퍼셉트론의 입력값과 가중치를 행렬로 표현해보면 다음과 같이 됩니다. (보통 벡터나 행렬은 굵은 글씨체로 나타냅니다.)
이런 식으로 두면 x와 y 행렬은 각각 1 x n 행렬이 되어 곱셈이 되지 않겠지요. 그래서 w를 n x 1 행렬로 바꾸어서 아래와 같이 곱을 정의하면 됩니다.
파이썬은 이런 형식의 벡터나 행렬연산을 아주 쉽게 해주는 훌륭한 도구가 있는데, 그게 바로 numpy 배열입니다. 결국 numpy는 다양한 차원의 행렬을 numpy 배열로 표현해서 numpy가 제공하는 다양한 메쏘드를 이용하면 번거로운 계산작업을 손쉽게 할 수 있습니다.
아무튼 입력값이나 가중치는 행렬로 취급하면 계산이 편리해지므로 행렬의 연산방법과 numpy에 대해 익숙해지면 좋겠지요~
>>> def predict(self, X):
return np.where(self.net_input(X) > self.thresholds, 1, -1)
self.net_input(X)의 값, 순입력 함수 결과값이 임계값인 self.thresholds의 값보다 크면 1, 그렇지 않으면 -1을 리턴하는 코드입니다. 따라서 이 함수는 활성 함수를 구현한 것입니다.
이제 AND 연산에 대해 퍼셉트론을 수행하는 perceptron_and.py 코드입니다.
perceptron_and.py
>>> from mylib.perceptron import Perceptron
mylib 폴더에 있는 perceptron.py에 있는 Perceptron 클래스를 임포트합니다.
>>> if __name__ == '__main__':
X = np.array([[0, 0], [0, 1], [1, 0], [1, 1]])
y = np.array([-1, -1, -1, 1])
ppn = Perceptron(eta=0.1)
ppn.fit(X, y)
print(ppn.error_)
X는 AND 연산에 대한 트레이닝 데이터를 정의한 것입니다. 트레이닝 데이터에 대한 실제 결과값에 대한 활성 함수 리턴값은 임계값 0보다 크면 1, 그렇지 않으면 -1이므로 y를 이 값들로 바로 정의합니다.
learning rate 에타값을 0.1로 두고 Perceptron 객체를 생성하고 이 객체의 fit() 멤버 함수를 호출함으로써 퍼셉트론 알고리즘을 구동합니다. perceptron_and.py를 구동하면 아래와 같은 학습 결과가 나옵니다.
[ 0.2 0.2 0.2]
[ 0. 0.4 0.2]
[-0.2 0.4 0.2]
[-0.2 0.4 0.4]
[-0.4 0.4 0.2]
[-0.4 0.4 0.2]
[-0.4 0.4 0.2]
[-0.4 0.4 0.2]
[-0.4 0.4 0.2]
[-0.4 0.4 0.2]
[1, 3, 3, 2, 1, 0, 0, 0, 0, 0]
이 결과를 보면 5번째 이후로 가중치의 업데이트가 발생하지 않기 때문에, 6번째 학습에서 AND 연산의 최종 학습이 마무리 되었다고 판단할 수 있습니다.
'책 리뷰 > Python Machine Learning' 카테고리의 다른 글
| [6편] 아달라인(Adaline)과 경사하강법(Gradient Descent) (0) | 2017.12.14 |
|---|---|
| [5편] 단순 인공신경망 퍼셉트론을 이용한 머신러닝 예시 (0) | 2017.12.14 |
| [3편] 파이썬으로 단순 인공신경망인 퍼셉트론 구현하기 (0) | 2017.12.14 |
| [2편] 퍼셉트론(Perceptron) - 인공신경망의 기초개념 (1) | 2017.12.14 |
| [1편] 인공지능과 머신러닝 (0) | 2017.12.14 |