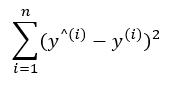(─━┘_└━─)/ 머리만1톤(Head1Ton)

import numpy as np
import re
from nltk.corpus import stopwords
stop = stopwords.words('english')
def tokenizer(text):
    text = re.sub('<[^>]*>', '', text)
    emoticons = re.findall('(?::|;|=)(?:-)?(?:\)|\(|D|P)', text.lower())
    text = re.sub('[\W]+', ' ', text.lower()) + ' '.join(emoticons).replace('-', '')
    tokenized = [w for w in text.split() if w not in stop]
    return tokenized

# generator 함수 stream_docs를 정의해서 한 번에 문서 하나를 읽어들이고 반환시키도록 한다.
def stream_docs(path):
    with open(path, 'r', encoding='utf-8') as csv:
        next(csv)
        for line in csv:
            text, label = line[:-3], int(line[-2])
            yield text, label

# 테스트로 movie_data.csv 파일의 첫 번째 문서를 읽어보자
print(next(stream_docs(path='movie_data.csv')))

# stream_docs 함수로부터 문서 스트림을 읽어들이고 size파라미터에 특정 문서의 숫자를 반환하는
# get_minibatch 함수를 정의
def get_minibatch(doc_stream, size):
    docs, y = [], []
    try:
        for _ in range(size):
            text, label = next(doc_stream)
            docs.append(text)
            y.append(label)
    except StopIteration:
        return None, None
    return docs, y

from sklearn.feature_extraction.text import HashingVectorizer
from sklearn.linear_model import SGDClassifier
vect = HashingVectorizer(decode_error='ignore', n_features=2**21, preprocessor=None, tokenizer=tokenizer)
clf = SGDClassifier(loss='log', random_state=1, n_iter=1)
doc_stream = stream_docs(path='movie_data.csv')

import pyprind
pbar = pyprind.ProgBar(45)
classes = np.array([0, 1])
for _ in range(45):
    X_train, y_train = get_minibatch(doc_stream, size=1000)
    if not X_train:
        break
    X_train = vect.transform(X_train)
    clf.partial_fit(X_train, y_train, classes=classes)
    pbar.update()

X_test, y_test = get_minibatch(doc_stream, size=5000)
X_test = vect.transform(X_test)
print('Accuarcy: %.3f' % clf.score(X_test, y_test))

clf = clf.partial_fit(X_test, y_test)

'''
머신러닝 모델을 웹 어플리케이션에 임베트하는 방법으로
데이터를 실시간으로 학습하는 방법을 익혀보자.
'''

# 피팅된 사이킷런 에스티메이터 직렬화
import pickle
import os

dest = os.path.join('movieclassifier', 'pkl_objects')
if not os.path.exists(dest):
    os.makedirs(dest)

pickle.dump(stop, open(os.path.join(dest, 'stopwords.pkl'), 'wb'), protocol=4)
pickle.dump(clf, open(os.path.join(dest, 'classifier.pkl'), 'wb'), protocol=4)

# vectorizer.py
from sklearn.feature_extraction.text import HashingVectorizer
import re
import os
import pickle

cur_dir = os.path.dirname(__file__)
stop = pickle.load(open(os.path.join(cur_dir, 'pkl_objects', 'stopwords.pkl'), 'rb'))

def tokenizer(text):
    text = re.sub('<[^>]*>', '', text)
    emoticons = re.findall('(?::|;|=)(?:-)?(?:\)|\(|D|P)', text.lower())
    text = re.sub('[\W]+', ' ', text.lower()) + ' '.join(emoticons).replace('-', '')
    tokenized = [w for w in text.split() if w not in stop]
    return tokenized

vect = HashingVectorizer(decode_error='ignore', n_features=2**21, preprocessor=None, tokenizer=tokenizer)


import pickle
import re
import os
#from vectorizer import vect
clf = pickle.load(open(os.path.join('pkl_objects', 'classifier.pkl'), 'rb'))


import numpy as np
label = {0:'negative', 1:'positive'}
example = ['I love this movie']
X = vect.transform(example)
print('Prediction: %s\nProbaility: %.2f%%' % (label[clf.predict(X)[0]], np.max(clf.predict_proba(X))*100))

pbar.py
import pyprind
import pandas as pd
import os
pbar = pyprind.ProgBar(50000)
labels = {'pos':1, 'neg':0}

df = pd.DataFrame()
'''
for s in ('test', 'train'):
    for l in ('pos', 'neg'):
        path = './aclImdb/%s/%s' % (s, l)
        for file in os.listdir(path):
            with open(os.path.join(path, file), 'r', encoding='utf-8') as infile:
                txt = infile.read()
            df = df.append([[txt, labels[l]]], ignore_index=True)
            pbar.update()

df.columns = ['review', 'sentiment']

import numpy as np
np.random.seed(0)
df = df.reindex(np.random.permutation(df.index))
df.to_csv('./movie_data.csv', index=False)
'''
df = pd.read_csv('./movie_data.csv')
print('df.head(3):\n', df.head(3))

# pbar 실행

# 단어를 피처 벡터로 변환
import pandas as pd
import numpy as np
df = pd.DataFrame()
df = pd.read_csv('./movie_data.csv')
print('df.head(3):\n', df.head(3))

from sklearn.feature_extraction.text import CountVectorizer
count = CountVectorizer()
docs = np.array([
    'The sun is shining',
    'The weather is sweet',
    'The sun is shining and the weather is sweet'
])
bag = count.fit_transform(docs)

print(count.vocabulary_)
print(bag.toarray())

'''
nd는 문서의 전체 개수, df(d,t)는 용어 t를 포함하는 문서 d의 개수
'''
from sklearn.feature_extraction.text import TfidfTransformer
tfidf = TfidfTransformer()
np.set_printoptions(precision=2)
print(tfidf.fit_transform(count.fit_transform(docs)).toarray())

print(df.loc[0, 'review'][-50:])

import re
def preprocessor(text):
    text = re.sub('<[^>]*>', '', text)
    emoticons = re.findall('(?::|;|=)(?:-)?(?:\)|\(|D|P)', text)
    text = re.sub('[\W]+', ' ', text.lower()) + ' '.join(emoticons).replace('-', '')
    return text

print(preprocessor(df.loc[0, 'review'][-50:]))
print(preprocessor("</a>This :) is :( a test :-)!"))

# 모든 영화 리뷰에 적용
df['review'] = df['review'].apply(preprocessor)

# 문서를 토큰으로 처리하기
def tokenizer(text):
    return text.split()
print('tokenizer:\n', tokenizer('running like running and thus they run'))

from nltk.stem.porter import PorterStemmer
porter = PorterStemmer()

def tokenizer_porter(text):
    return [porter.stem(word) for word in text.split()]

print('tokenizer_porter("runners like running and thus they run"):\n'
      , tokenizer_porter('runners like running and thus they run'))

'''
불용어(stop-word) : 모든 종류의 텍스트에서 공통으로 많이 사용되는 단어들로 문서의 다른 종류들을 구별하는 데
유용할 만한 정보를 거의 가지고 있지 않은 (혹은 아주 조금만 가지고 있는) 경우를 말한다.
불용어의 예로는 is, and, has 같은 것들이 있다.
'''
import nltk
nltk.download('stopwords')

from nltk.corpus import stopwords
stop = stopwords.words('english')
[print(w) for w in tokenizer_porter('a runner likes running and runs a lot')[-10:] if w not in stop]

# 문서 분류를 위한 로지스틱 회귀 모델 훈련
X_train = df.loc[:25000, 'review'].values
y_train = df.loc[:25000, 'sentiment'].values
X_test = df.loc[25000:, 'review'].values
y_test = df.loc[25000:, 'sentiment'].values

# GridSearchCV 오브젝트를 사용하여 5-폴드(5-fold) 충화 교차검증을
# 사용하는 이번 로지스틱 회귀 모델에 대한 최적의 파라미터 세트를 찾아보자
from sklearn.grid_search import GridSearchCV
from sklearn.pipeline import Pipeline
from sklearn.linear_model import LogisticRegression
from sklearn.feature_extraction.text import TfidfVectorizer
tfidf = TfidfVectorizer(strip_accents=None, lowercase=False, preprocessor=None)
param_grid = [{'vect__ngram_range': [(1,1)],
               'vect__stop_words': [stop, None],
               'vect__tokenizer': [tokenizer, tokenizer_porter],
               'clf__penalty': ['l1', 'l2'],
               'clf__C': [1.0, 10.0, 100.0]},
              {'vect__ngram_range': [(1,1)],
               'vect__stop_words': [stop, None],
               'vect__tokenizer': [tokenizer, tokenizer_porter],
               'vect__use_idf': [False],
               'vect__norm': [None],
               'clf__penalty': ['l1', 'l2'],
               'clf__C': [1.0, 10.0, 100.0]}]
lr_tfidf = Pipeline([('vect', tfidf),
                     ('clf', LogisticRegression(random_state=0))])
gs_lr_tfidf = GridSearchCV(lr_tfidf, param_grid, scoring='accuracy', cv=5, verbose=1, n_jobs=1)
gs_lr_tfidf.fit(X_train, y_train)
print('Best parameter set : %s ' % gs_lr_tfidf.best_params_)

print('CV Accuracy: %.3f' % gs_lr_tfidf.best_score_)
clf = gs_lr_tfidf.best_estimator_
print('Test Accuracy: %.3f' % clf.score(X_test, y_test))

import numpy as np
import re
from nltk.corpus import stopwords
stop = stopwords.words('english')
def tokenizer(text):
    text = re.sub('<[^>]*>', '', text)
    emoticons = re.findall('(?::|;|=)(?:-)?(?:\)|\(|D|P)', text.lower())
    text = re.sub('[\W]+', ' ', text.lower()) + ' '.join(emoticons).replace('-', '')
    tokenized = [w for w in text.split() if w not in stop]
    return tokenized

# generator 함수 stream_docs를 정의해서 한 번에 문서 하나를 읽어들이고 반환시키도록 한다.
def stream_docs(path):
    with open(path, 'r', encoding='utf-8') as csv:
        next(csv)
        for line in csv:
            text, label = line[:-3], int(line[-2])
            yield text, label

# 테스트로 movie_data.csv 파일의 첫 번째 문서를 읽어보자
print(next(stream_docs(path='./machinelearning/movie_data.csv')))

# stream_docs 함수로부터 문서 스트림을 읽어들이고 size파라미터에 특정 문서의 숫자를 반환하는
# get_minibatch 함수를 정의
def get_minibatch(doc_stream, size):
    docs, y = [], []
    try:
        for _ in range(size):
            text, label = next(doc_stream)
            docs.append(text)
            y.append(label)
    except StopIteration:
        return None, None
    return docs, y

from sklearn.feature_extraction.text import HashingVectorizer
from sklearn.linear_model import SGDClassifier
vect = HashingVectorizer(decode_error='ignore', n_features=2**21, preprocessor=None, tokenizer=tokenizer)
clf = SGDClassifier(loss='log', random_state=1, n_iter=1)
doc_stream = stream_docs(path='./machinelearning/movie_data.csv')

import pyprind
pbar = pyprind.ProgBar(45)
classes = np.array([0, 1])
for _ in range(45):
    X_train, y_train = get_minibatch(doc_stream, size=1000)
    if not X_train:
        break
    X_train = vect.transform(X_train)
    clf.partial_fit(X_train, y_train, classes=classes)
    pbar.update()

X_test, y_test = get_minibatch(doc_stream, size=5000)
X_test = vect.transform(X_test)
print('Accuarcy: %.3f' % clf.score(X_test, y_test))

clf = clf.partial_fit(X_test, y_test)

그동안 개인적으로 이런저런 일로 바쁘고, 많은 변화가 있어, 정말 오랜만에 포스팅을 하게 됩니다.

이번 포스팅에서는 여태까지 다루어 보았던 머신러닝 및 딥러닝, AI와 관련하여 그 기반이 되는 인공신경망에 대한 간략한 히스토리를 정리해보고자 합니다.

​

​아, 물론 딥러닝의 꽃이라 부를 수 있는 CNN(Convolutional Neural Network)이나 RNN(Recurrent Neural Network) 등에 대해서는 제 블로그에서 아직 다루진 않았습니다만... 이에 대해서는 시간 나는대로 포스팅하도록 하겠습니다.

먼저 아래 그림으로 인공신경망에 대한 간략한 히스토리를 정리해봅니다.

그러면 위 그림을 보면서 인공신경망 발전의 역사를 살포시 살펴봅니다. (내용중 재탕하는 내용도 있으니 참고바랍니다.)

1943년 신경과학자인 Warren S. McCulloch과 논리학자인 Walter Pitts는 하나의 사람 뇌 신경세포를 하나의 이진(Binary)출력을 가지는 단순 논리 게이트로 설명했는데, 이를 McCulloch-Pitts 뉴런(MCP 뉴런)이라 부릅니다.

1957년 코넬 항공 연구소에 근무하던 Frank Rosenblatt은 MCP 뉴런 모델을 기초로 퍼셉트론(Perceptron) 학습 규칙이라는 개념을 고안하게 되는데, Rosenblatt은 하나의 MCP 뉴런이 출력신호를 발생할지 안할지 결정하기 위해, MCP 뉴런으로 들어오는 각 입력값에 곱해지는 가중치 값을 자동적으로 학습하는 알고리즘을 제안했습니다.

1958년 퍼셉트론이 발표된 후 같은 해 7월 8일자 뉴욕타임즈는 앞으로 조만간 걷고, 말하고 자아를 인식하는 단계에 이르는 컴퓨터 세상이 도래할 것이라는 다소 과격한 기사를 냈습니다.

​

하지만 1969년, 단순 퍼셉트론은 ​XOR 문제도 풀 수 없다는 사실을 MIT AI 랩 창시자인 Marvin Minsky 교수가 증명하였고, 아래 그림과 같은 다층 퍼셉트론(MLP)으로 신경망을 구성하면 XOR 문제를 풀 수 있다고 했습니다. 

그런데, Minsky 교수는 이러한 MLP에서 hidden layer의 가중치를 계산하는, 다시 말하면 MLP를 학습시키는 방법은 존재하지 않는다고 단정해버렸습니다.

이로 인해 떠들석했던 인공신경망과 관련된 학문과 기술은 더 이상 발전되지 않고 암흑기를 겪게 됩니다.

그러다가 1974년, 당시 하버드 대학교 박사과정이었던 Paul Werbos는 MLP를 학습시키는 방법을 찾게 되는데, 이 방법을 Minsky 교수에게 설명하지만 냉랭한 분위기속에 무시되버립니다.

Paul Werbos가 Minsky 교수에게 설명한 MLP를 학습시킬 수 있는 획기적인 방법이 바로 오류 역전파 (Backpropagation of errors)라는 개념입니다. 그냥 줄여서 역전파(Backpropagation)이라 부르기도 하지요.

​

이런 획기적인 방법 역시 당시 인공신경망의 대가와 학계로부터 무시당해버린 후 Werbos는 1982년 역전파에 대한 내용을 논문으로 발표하고 마무리합니다. Werbos의 역전파가 무시된 이후 10여년 넘게 AI 분야는 혹한기를 겪게 됩니다.

그러다가 1986년 인지심리학자이자 컴퓨터공학자였던 Geoffrey Hinton 교수는 Werbos가 제안한 오류 역전파 알고리즘에 대한 내용을 독자적으로 제안하게 됩니다. 하지만 Werbos가 수 년전에 먼저 논문으로 발표한 내용이기 때문에 Hinton 교수는 역전파 개념을 다시 발견했다고 보는 것이 맞을 겁니다.

그런데 다층구조로 되어 있는 MLP의 학습은 역전파를 통해 학습이 가능하지만 학습의 효과를 크게 하려면 인공신경망의 은닉층(hidden layer)를 많이 쌓아야 더 좋은 결과가 나올 수 있다는 것이 경험적으로 검증되었습니다.

하지만, 당시까지만 해도 활성함수로써 시그모이드 함수를 사용했고, 이는 은닉층의 개수가 많아질수록 역전파에 의한 가중치 계산이 불가능하게 되는 gradient vanishing이라는 문제에 직면하게 되었습니다.

​

gradient vanishing 문제는 인공신경망 분야의 2번째 암흑기가 시작되는 계기가 되버립니다.

1995년에는 당시 다른 방식으로 발전되었던 보다 단순한 머신러닝 알고리즘인 SVM, RandomForest와 같은 알고리즘이 손글씨 인식 등과 같은 분야에는 더 잘 작동한다고 Lecun 교수 등이 발표하기도 했습니다.

​

1998년 컴퓨터공학자인 Yann Lecun 교수는 1950년대 수행했던 고양이의 뇌파 실험에 영감을 얻어 이미지 인식을 획기적으로 개선할 수 있는 CNN(Convolutional Neural Network)라는 새로운 형태의 인공신경망을 고안하게 됩니다.

1950년대 수행했던 고양이의 실험은 고양이의 눈으로 보는 사물의 형태에 따라 뇌의 특정영역, 정확히 말하면 특정 뉴런만이 활성화 된다는 것을 알게 된 것입니다. Lecun 교수는 이러한 실험 결과에 영감을 얻어 CNN이라는 새로운 형태의 인공신경망을 고안하게 된 것입니다.

하지만 gradient vanishing 문제 등으로 인해 한동안 인공신경망 분야가 침체기를 겪고 있던 시기에, Hinton 교수와 Bengio 교수는 2006년, 2007년 두 편의 논문을 발표하였는데 초기 입력값을 잘 선택하면 아무리 인공신경망의 층의 개수가 많더라도 학습이 가능하며, 복잡한 문제도 층의 개수가 많게 구성된 인공신경망이라면 해결할 수 있다고 했습니다. 그리고 이렇게 층의 개수가 많은 신경망을 심층신경망(Deep Neural Network:DNN)이라 리브랜딩하고 심층신경망을 학습시키는 방법을 딥러닝(Deep Learning:DL)이라고 명명하게 됩니다.

그리고 2000년 네이처(Nature)지에 시그모이드를 대신하여 사용한 Rectifier라는 활성함수를 이용해 효과를 봤다는 내용의 생물학 분야의 논문이 발표되었습니다. Rectifier는 ReLU(Rectified Linear Unit)라고 불리게 되는 활성함수인데, 이 활성함수를 심층신경망의 딥러닝에 사용해보니 gradient vanishing 문제가 해결되버린 것입니다. 물론 심층신경망의 최종 출력층에서는 여전히 시그모이드나 SoftMax를 사용하지만 말이죠.

아무튼 활성함수 ReLU의 등장으로 딥러닝은 많은 발전을 이루게 되었고, 2012년 이미지 인식 분야의 유명한 대회인 ImageNet Large Scale Visiual Recognition Challenge(ILVRC)에서 캐나다 토론토 대학의 AlexNet이라 불리는 CNN 인공신경망으로 우승하게 되는데, 이전 까지 이미지 인식 오류율이 26%대였던 것이 15%대로 줄이게 된 것입니다.

이후 CNN의 신경망구조가 지속적으로 개선되고 GPU의 발전으로 현재는 5% 이내의 오류율로 학습이 가능하게 되었습니다.

현재 이미지 인식 수준은 아래 그림과 같이 주어진 사진을 설명하는 단계에 이르고 있습니다.

그리고 2016년 알파고가 등장하여 이세돌 9단을 4승1패로 이기면서 세계를 놀라게 했고, 현재는 인공신경망을 이용한 인공지능을 자율주행자동차와 같은 다양한 분야에 적용하고자 노력하고 있는 중입니다.

​

​        

​

아마, 미래에는 스스로 생각하고 인지하는 인공지능이 탄생할지도 모르지요.

하지만....

아직까지 인공지능과 우리 인간의 뇌는 다릅니다!

• 인간의 뇌는 약 1천억개의 뉴런과 100조개의 시냅스로 연결되어 있고, 20와트의 전력만으로 충분합니다.
• 하지만 가장 거대한 인공신경망의 규모는 기껏해봐야 16,000개의 CPU코어상에서 1천만 뉴런과 10억개의 연결로 이루어져 있으며, 소모되는 전력은 3백만와트나 됩니다.
• 인간의 뇌는 5개의 감각기관으로부터 5가지 유형의 입력만 받습니다.
• 우리 아기들은 고양이를 학습하는데 라벨링된 10만장의 사진이 필요하지 않습니다.

솔직히 우리는,,, 학습이 이루어지는 우리 뇌의 기작을 잘 알지 못합니다.

이상으로 인공신경망에 대한 히스토리를 가볍게 살펴보았습니다.

아래 영상은 제가 ImageNet으로부터 다운받은 강아지 사진과 꽃 사진을 이용해 tensorflow로 학습을 하고 구글에서 제공해준 템플릿 코드를 이용하여 만들어본 안드로이드 프로그램을 구동한 것입니다.

왼쪽 동영상은 제 스마트폰으로 PC화면에 보이는 강아지와 꽃들을 촬영한 화면을 캡쳐 녹화한 것이고, 오른쪽 동영상은 우리집 강아지와 장미 조화를 스마트폰으로 촬영한 영상을 보인 것입니다. 화면에 표시되는 숫자는 이미지 인식 확률이며 1.0이 100%입니다.  

참고로 제 사진 50여장과 무작위 남자 사진 1000여장을 학습시켜본 결과 제 사진을 촬영했을 때 저를 인식한 확률이 매우 높았습니다.  

다층 퍼셉트론과 같은 인공신경망을 구현하는 것은 꽤 복잡하고 까다로운 작업이라는 것을 [37편]에서 잠시 느꼈을 것입니다. 그렇다면 우리가 구현한 인공신경망이 제대로 동작하는지, 혹은 정확도가 얼마인지 어떻게 측정해야 할까요?

인공신경망 구현의 핵심은 역전파라고 했으니, 역전파 알고리즘이 얼마나 정확하게 구현되었는지에 대해 검증하면 될 것 같습니다. 역전파 알고리즘을 우리가 직접 수동으로 검증하는 방법이 그라디언트 체킹(gradient checking)이라는 기법입니다.

이번 포스팅에서는 그라디언트 체킹에 대해 가볍게 살펴보고 넘어갑니다.

역전파에서 가중치를 업데이트하기 위해 계산해야 하는 식은 아래의 편미분 식이라는거 이미 알고 있습니다.

여기서 w는 신경망의 모든 가중치에 대한 행렬입니다. 이 미분값을 해석적 그라디언트(Analytical Gradient) 값이라 부릅니다.

도함수의 정의에 의해 해석적 그라디언트는 아래와 같이 표현됩니다.

[식1] 

[식1]의 오른쪽 항에서 ε이 매우 작은 값이라 할 때, 아래의 값으로 근사됩니다.

[식2] 

[식2]의 오른쪽 항의 값을 수치적 그라디언트(Numerical Gradient) 값이라 부릅니다.

아래 그림은 수치적 그라디언트의 기하학적인 의미를 나타낸 것입니다.

[식2]에서 ε을 -ε으로 바꾸어보면 아래의 식이 됩니다.

[식3]

[식2]와 [식3]의 양 변을 각각 더하면 아래의 식이 됩니다.

따라서,

[식4]

[식4]의 오른쪽 항을 새롭게 정의한 수치적 그라디언트로 채택합니다. 실제로 새롭게 정의한 수치적 그라디언트가 해석적 그라디언트와의 오차가 더 작게 나옵니다. 

수치적 그라디언트를 J'n 이라 하고 해석적 그라디어트를 J'a라 하면 절대오차 Err와 상대오차 Rerr는 다음과 같이 정의합니다.

[식5]

이 식에서 || ||는 행렬의 놈(norm)이며 행렬의 놈은 행렬의 모든 성분을 p제곱하여 더한 값의 p제곱근으로 정의됩니다.

n x m 행렬 A가 다음과 같을 때,

​

​

행렬 A의 놈은 아래와 같이 정의됩니다.

여기서 p=2인 경우를 프로베니우스 놈이라 부르며 가장 일반적으로 많이 사용되는 행렬 놈입니다.

우리가 구현한 역전파 알고리즘의 정확도는 해석적 그라디언트와 수치적 그라디언트의 상대 오차값으로 평가합니다. 역전파 알고리즘의 정확도를 평가하는 측도로써 절대 오차를 사용하지 않는 이유는 Err가 매우 작은 값이더라도 J'n, J'a  값 자체가 매우 작다면 상대적으로 오차율이 커지기 때문입니다.

상대오차 Rerr의 값에 따른 역전파 알고리즘의 정확도는 일반적으로 아래와 같은 규칙을 따릅니다.

이 규칙에 따라 [37편]에서 구현한 MLP를 검증해보도록 합니다.

아래의 코드를 [37편]의 dl_mlp_class.py에서 구현한 NeuralNetMLP 클래스의 메쏘드로 추가합니다.

이 코드는 [식5]의 Rerr를 계산하여 리턴하는 함수를 구현한 것입니다. 코드를 보면 그렇게 어려운 부분이 없습니다.

NeuralNetMLP 클래스의 fit() 메쏘드에서 역전파를 통해 경사를 계산하는 코드를 찾습니다.

이 코드 다음에 아래의 코드를 추가합니다.

그라디언트 체크 기능이 추가된 NeuralNetMLP 클래스가 완성되었습니다. 이제 아래의 코드를 작성합니다.

이 코드는 X_train, y_train의 5개 데이터에 대한 10회 학습의 그라디언트 체킹을 수행한 결과를 화면에 출력합니다. 시간이 제법 소요되므로 너긋하게 기다리면서 결과를 지켜보도록 합니다.

코드를 수행한 결과는 다음과 같습니다.

Warning: 3.537822909e-07
OK: 3.02628344172e-10
OK: 3.02609921621e-10
OK: 3.06158619281e-10
OK: 3.21874437906e-10
OK: 3.27658507646e-10
OK: 2.87684685361e-10
OK: 2.32833603418e-10
OK: 2.52932883134e-10
OK: 2.70109334393e-10

1회 학습을 빼고 2회~10회까지 그라디언트 체킹 결과는 매우 훌륭하다는 것을 알 수 있습니다. 따라서 [37편]에서 구현한 역전파 알고리즘은 제대로 구현한 것이라고 판단할 수 있습니다.

체킹이 마무리되면 fit()에 추가한 그라디언트 체킹 수행 코드를 주석 처리 해둡니다. 

이번 포스팅에서는 [34편]~[36편] 내용에서 다룬 다층 퍼셉트론을 파이썬으로 구현한 코드를 소개하고, MNIST의 손글씨 숫자 60,000개의 샘플을 딥러닝 학습을 수행한 후 손글씨 숫자에 대한 인식률을 살펴보는 것으로 하겠습니다.

MNIST 데이터는 다양한 사람들이 직접 쓴 숫자 0~9까지의 이미지 집합이며, 이미지의 크기는 28 x 28 크기로 표준화되어 있습니다. MNIST 데이터는 트레이닝을 위한 60,000개의 손글씨 숫자 이미지 데이터와 테스트를 위한 10,000개의 손글씨 숫자 이미지 데이터로 구성되어 있습니다.

먼저 아래의 링크를 눌러서 MNIST 데이터를 확보합니다.

☞ MNIST 데이터 받기

링크를 눌러 MNIST 데이터 홈페이지에 들어가면 아래와 같은 4개의 데이터 파일이 보일 것입니다.

• train-images-idx3-ubyte.gz : training set images
• train-labels-idx1-ubyte.gz : training set labels
• t10k-images-idx3-ubyte.gz : test set images
• t10k-labels-idx1-ubyte.gz : test set labels

이 파일들을 모두 다운로드 받아 특정 디렉토리에 저장한 후, 압축 프로그램을 이용해 압축을 해제합니다.

MNIST 데이터 홈페이지 아랫부분에 보면 이 파일들에 대한 포맷형식이 설명되어 있습니다. 파일 포맷을 요약해보면 다음과 같습니다.

TRAINING SET LABEL FILE (train-labels-idx1-ubyte):

[offset] [type]          [value]          [description] 
0000     32 bit integer  0x00000801(2049) magic number (MSB first) 
0004     32 bit integer  60000            number of items 
0008     unsigned byte   ??               label 
0009     unsigned byte   ??               label 
........ 
xxxx     unsigned byte   ??               label

※label 값은 0~9까지임

TRAINING SET IMAGE FILE (train-images-idx3-ubyte):

[offset] [type]          [value]          [description] 
0000     32 bit integer  0x00000803(2051) magic number 
0004     32 bit integer  60000            number of images 
0008     32 bit integer  28               number of rows 
0012     32 bit integer  28               number of columns 
0016     unsigned byte   ??               pixel 
0017     unsigned byte   ??               pixel 
........ 
xxxx     unsigned byte   ??               pixel

※ 픽셀값은 1바이트씩 아래로 쭉 연결됨. 28x28=784바이트 단위로 하나의 손글씨 이미지로 구분되며 pixel값이 0이면 흰색 바탕, 255이면 검정색 숫자 부분을 의미함

테스트를 위한 파일 포맷도 트레이닝 데이터와 마찬가지 포맷입니다. 트레이닝을 위한 라벨 데이터가 저장된 파일의 최초 8바이트에는 아이템 개수 등의 정보가 저장되어 있고 라벨은 9바이트째부터 시작됩니다. 손글씨 숫자 이미지가 저장된 파일의 최초 16바이트에는 이미지 개수, 가로 세로 픽셀수 등의 정보가 저장되어 있고 이미지 픽셀 데이터는 17바이트째부터 시작됩니다.

자, 그럼 아래의 코드를 봅니다.

dl_load_digits.py

위 코드의 load_mnist(path, kind='train')는 라벨 데이터가 저장된 파일과 이미지 데이터가 저장된 파일로부터 데이터를 모두 읽어 각각 numpy 배열 labels, images로 저장하여 리턴하는 함수입니다.

참고로 이 포스팅에서는 학습을 위한 데이터가 저장된 폴더는 dl_load_digits.py가 저장된 폴더 아래에 data/mnist 폴더입니다. 따라서 여러분들의 학습 데이터가 저장된 폴더 위치에 맞게 경로를 조정해줘야 한다는 거 잊지마세요~

코드에 등장하는 struct.unpack()은 저의 첫번째 책 '암호와 해킹'에서 간략하게 설명되어 있는데, 간단히 요약하여 설명하면, 파이썬의 struct 모듈은 파이썬 바이트 객체로 표현된 C구조체와 파이썬에서 사용하는 값을 상호 변환하는데 사용되는 각종 메쏘드들을 제공합니다.

>>> magic, n = struct.unpack('>II', imgpath.read(8))

이 코드의 의미는 imgpath 파일에서 8바이트 데이터를 big-endian(>)으로 읽고, 읽은 데이터를 unsigned integer(I) 2개로 나누어서 각각 magic, n 변수에 대입하라는 뜻입니다. 

이 코드를 실행하면 4개의 MNIST 데이터 파일을 모두 읽어, 트레이닝 이미지 데이터는 X_train, 트레이닝 라벨 데이터는 y_train, 테스트 이미지 데이터는 X_test, 테스트 라벨 데이터는 y_test로 저장하고 이미지 샘플의 개수 정보를 화면에 표시합니다.

코드를 실행하면 다음과 같은 결과가 나오면 데이터를 성공적으로 로드한 것입니다.

학습 샘플수     : 60000, 컬럼수: 784

테스트 샘플수  : 10000, 컬럼수: 784

이제, 아래의 코드를 dl_load_digits.py 아래 부분에 추가합니다.

dl_show_09digits.py

이 코드는 X_train에 저장된 0~9까지 이미지를 화면에 출력하는 코드입니다. 코드를 실행하면 다음과 같은 손글씨 숫자가 화면에 나올 겁니다.

위 코드를 아래와 같이 약간 수정해서 같은 숫자 25개에 대한 이미지를 화면에 출력하도록 해봅니다.

dl_show_samedigits.py

이 코드를 실행하면 아래와 같이 숫자 6에 대한 다양한 손글씨 이미지 25개를 화면에 출력합니다.

dl_show_samedigits.py 코드에서 y_train == 6 부분을 y_train == 5 등으로 바꾸어 다른 숫자들도 확인해보세요. 이로써 우리가 확보한 MNIST 손글씨 데이터가 어떤 식으로 되어있는지 확인을 했네요~

이제는 이 손글씨 데이터를 학습할 다층 퍼셉트론을 파이썬으로 구현하는 것입니다. 이 포스팅에 제시된 대부분의 소스코드는 Sebatian Raschka의 책 "Python Machine Learning"에서 발췌한 것이며 필요시 제가 조금 수정하거나 추가한 코드도 있기도 합니다. 아래에 제시된 MLP 구현 코드도 이 책에서 발췌한 것인데, 딥러닝 성능을 위해 추가적인 알고리즘이 적용되어 있는 제대로 된 다층 퍼셉트론을 구현한 코드입니다. 

dl_mlp_class.py

음... 코드가 참 깁니다. 딥러닝의 세계는 쉽지 않은 길입니다. NeuralNetMLP라는 이름의 클래스가 바로 다층 퍼셉트론을 구현한 부분입니다. 코드의 세부적인 내용을 이 포스팅에서 일일이 서술하는 것은 무리일 것 같아서, 함수 단위로 설명을 하도록 합니다.

먼저, NeuralNetMLP 클래스의 초기값을 위해 입력되는 인자들이 굉장히 많습니다. 이 인자들에 대해 가볍게 살펴보는 것으로 시작해봅니다.

• n_output:
• 출력층의 출력값 개수. 손글씨 숫자의 경우 0~9까지 10으로 지정하면 됨
• n_features:
• 입력층에 입력되는 특성값의 개수. 28x28 픽셀의 이미지 데이터이므로 784로 지정하면 됨
• n_hidden:
• 은닉층의 노드 개수. 손글씨 숫자 학습을 위해 50으로 지정할 것임
• l1:
• L1 정규화를 위한 람다값. 오버피팅 방지를 위한 것임
• l2:
• L2 정규화를 위한 람다값. 오버피팅 방지를 위한 것임
• epochs:
• 학습 반복 회수
• eta:
• learning rate η
• alpha:
• 가중치 업데이트를 보다 고속으로 처리하기 위한 모멘텀 학습 파라미터
• decrease_const:
• 학습 수렴률을 향상시키기 위해 learning rate을 학습 반복에 따라 감소시키기 위한 감쇠 상수
• 처음에는 learning rate을 다소 큰 값으로 잡아 최소값에 빨리 다다르게 한 후, 감쇠 상수를 ​지속적으로 곱해서 learning rate을 점점 작아지게 할 용도로 사용됨
• shuffle:
• 매 반복마다 트레이닝 데이터를 뒤섞기를 위한 플래그. True이면 뒤섞음
• minibatches:
• 매 학습에 사용되는 무작위로 추출할 트레이닝 데이터의 실제 개수. 확률적 경사하강법 적용 개념임
• 모집단에서 일정 크기의 표본을 추출하여 ​결과를 통계적으로 예측하는 것과 비슷한 개념

이것으로 NeuralNetMLP의 초기화를 위한 인자에 대해 설명했습니다. 보면 우리가 아직 다루지 않은 모멘텀 학습 파라미터라든가 감쇠 상수 같은 내용도 있는데, 그냥 이런 것들이 있다는 것만 알고 넘어갑니다.

​아무튼 NeuralNetMLP는 [34편], [35편], [36편]에서 다룬 내용을 코드화 한 것으로 볼 수 있습니다.

이제 NeuralNetMLP의 각 함수에 대해 가볍게 설명합니다.

• _encode_labels(self, y, k)
• 출력층 10개 노드에서 출력되는 값이 (1, 0,...0)이면 0, (0, 1, 0,,,)이면 1, (0, 0, ...,1)이면 9를 의미하는 것으로 정의함
• y는 손글씨 숫자의 라벨링 데이터, k는 출력층의 출력값 개수

• _initialize_weights(self)
• 입력층과 은닉층 사이의 가중치 w1과 은닉층과 출력층 사이의 가중치 w2의 값을 초기화함. 바이어스 항도 포함시킴

• _sigmoid(self, z)
• z에 대한 시그모이드 함수값을 리턴함. scipy.expit()은 시그모이드 함수임

• _sigmoid_gradient(self, z)
• z에 대한 시그모이드 함수의 미분값을 리턴함.

• _add_bias_unit(self, X, how='column')
• X에 바이어스 값을 추가해서 X_new로 둠. 행렬 계산의 특성상 입력층에서 은닉층, 은닉층에서 출력층으로의 계산을 위해 how 값을 'column', 'row'로 지정하여 바이어스를 행에 더하거나, 열에 더하도록 함

• _feedforward(self, X, w1, w2)
• w1, w2 가중치로 X를 순전파 시킵니다. 순전파한 결과는 a1, z2, a2, z3, a3로 리턴함

• _L2_reg(self, lambda_, w1, w2), _L1_reg(self, lambda_, w1, w2)
• L2 정규화와 L1 정규화 값을 리턴함

• _get_cost(self, y_enc, output, w1, w2)
• 로지스틱 비용함수 J를 리턴함. J에는 정규화를 위한 값이 추가되었음

• _get_gradient(self, a1, a2, a3, z2, y_enc, w1, w2)
• 역전파 알고리즘을 구현한 함수

• predict(self, X)
• X에 대한 예측값을 리턴

• fit(self, X, y, print_progress=True)
• 트레이닝 데이터 X, y를 이용해 다층 퍼셉트론을 학습시킴. 학습의 속도를 위해 minibatches로 지정된 개수만큼 데이터를 무작위로 추출하여 학습을 시킴 

코드의 세부적인 내용은 언급안했으나, 각 함수들의 역할과 이전 포스팅 [34편]~[36편]에서 다루었던 내용을 참고하여 코드를 다시 한번 보면 코드의 내용을 이해할 수 있을 것입니다.

이 코드를 dl_load_digits.py 맨 마지막 부분에 추가합니다.

이제는 구현한 다층 퍼셉트론으로 60,000개의 데이터에 대해 학습을 수행하는 코드를 볼 차례입니다.

dl_mlp_learning.py

이 코드는 결국 784-50-10 다층 퍼셉트론을 구성하고 50개의 데이터를 무작위로 추출한 후 1000번 반복 학습을 수행하는 코드입니다. 학습을 수행하는데 소요되는 시간은 컴퓨터의 성능에 따라 10~30분정도 소요됩니다. 한번 학습한 것을 또 학습할 수는 없으므로 pickle을 이용해 학습된 mlp 객체를 파일로 저장하여 나중에 다시 불러 사용할 수 있게 합니다.

추가한 코드를 실행합니다. 시간이 걸리므로 잠시 다른 일을 하고 와도 됩니다.

학습이 종료되면 학습 결과가 mlp_digits.pkl로 저장됩니다. 이 파일을 불러오려면 아래의 코드를 활용합니다.

dl_load_mlpobj.py

사용법은 이렇습니다. 여태까지 작성된 코드에서 dlp_mlp_learning.py 코드 부분은 주석 처리해서 나중에 트레이닝 데이터가 갱신되게 되면 재사용할 수 있도록 합니다. 그런 후, 주석 처리된 코드 아랫 부분에 dl_load_mlpobj.py 코드를 추가합니다. 이게 끝입니다. 이젠 10분 이상 걸리는 학습을 더 이상 수행하지 않아도 됩니다.

이제 학습의 결과가 어떠한지 살펴볼까요~. 일단 비용함수 J가 어떤 식으로 변화하는지 그래프로 살펴봅니다. 아래의 코드를 여태까지 작성한 코드 마지막 부분에 추가합니다.

dl_plot_cost1.py

추가한 코드를 실행하면 다음과 같은 결과가 화면에 나옵니다.

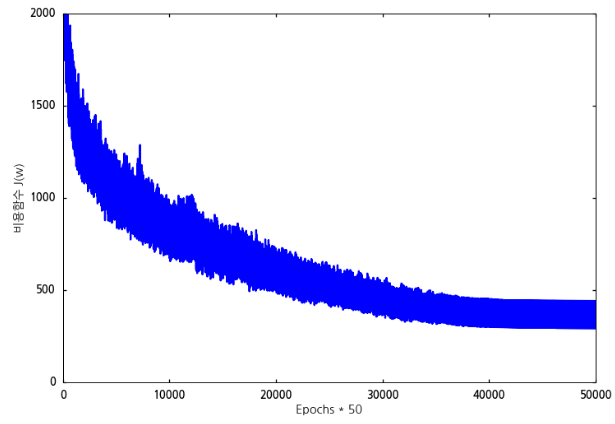
이 그래프는 실제로 비용함수의 값이 오르락 내리락 하는 그래프인데 실제로 그렇게 보이지 않네요. 아무튼 비용함수의 값이 오르락 내리락하면서 편차가 심합니다. 하지만 40,000번째 이후에는 오르락 내리락 하면서도 일정한 범위로 수렴한다는 것을 볼 수 있습니다.

그런데 이 녀석은 minibatches의 단위 50개의 데이터를 처리하는 과정에서 매회 비용함수를 계산한 것입니다. x축의 값을 보면 1,000번 반복한 것이 아니라 50,000번 반복한 것으로 나오는 이유입니다. 따라서 50개의 데이터를 처리한 것의 평균 비용함수의 값을 그래프로 나타내 봅니다.

dl_plot_cost1의 코드를 다음과 같이 수정합니다.

dl_plot_cost2.py

수정된 코드를 실행하면 다음과 같은 결과가 나옵니다.

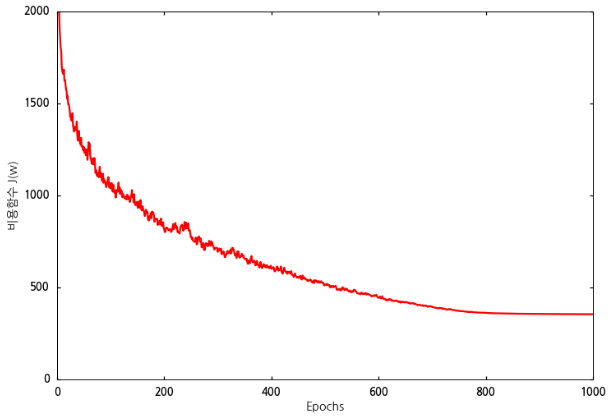
그래프를 보면 800회 학습 이후에 비용함수가 특정값으로 수렴하고 있음을 알 수 있습니다.

이제는 학습된 결과를 살펴보도록 합니다. 아래는 60,000개의 학습 데이터를 이용해 학습을 시키고 학습 데이터에 대한 학습 정확도를 계산하는 코드입니다. 

dl_mlp_predict_train.py 

이 코드를 실행하면 다음과 같은 결과가 나옵니다.

예측성공/총개수: [58680]/[60000]

딥러닝 정확도: 97.80%

dl_mlp_predict1.py를 조금 수정하여 테스트 데이터에 대한 정확도를 계산해봅니다.

dl_mlp_predict_test.py

이 코드를 실행하면 다음과 같은 결과가 나옵니다.

예측성공/총개수: [9597]/[10000]
딥러닝 정확도: 95.97%

두 개의 결과를 비교해보면 테스트 데이터에 대한 정확도가 트레이닝 데이터에 대한 정확도보다 쪼금 작습니다. 이는 학습 결과가 약간 오버피팅이 되었음을 알 수 있습니다.

그렇다면 어떤 손글씨 숫자들이 제대로 인식이 안되었는지 확인해보죠~

아래의 코드를 여태까지 작성한 코드 마지막에 추가합니다.

위 코드를 추가한 코드를 실행하면 아래와 같은 결과가 화면에 보입니다.

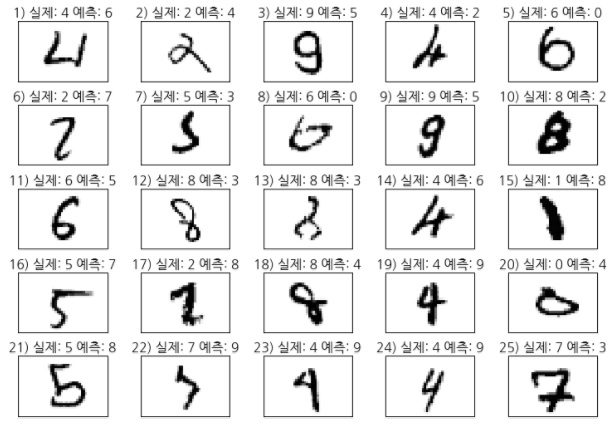
우리가 학습시킨 MLP가 잘못 인식한 숫자들 중 일부입니다. 그런데, 일부 숫자는 사람이 보기에도 구분이 안되는 것이 있습니다. 1), 6), 7), 8), 13), 17), 22), 23), 25) 등은 우리 눈으로 보기에도 헷갈리는 숫자들입니다.

아무튼 이런 데이터들에 대해서는 사용자로 하여금 피드백을 줘서 제대로 된 숫자로 인식하도록 학습시키면 될 것입니다. 사용자의 피드백을 재학습시키는 내용에 대해서는 [22편] 마지막 부분에서 다루었습니다.  

만약 여러분들이 직접 쓴 숫자를 여기서 학습한 MLP를 이용해 인식하려고 하면 아래와 같은 로직으로 프로그램을 작성하면 됩니다.

1. 여러분이 손으로 쓴 숫자를 이미지로 저장합니다.
2. 이미지의 크기를 OpenCV의 cv2.resize()를 이용해 28 x 28 크기로 변환합니다.
3. OpenCV의 cv2.threshold()를 이용해 숫자 부분과 배경부분을 검정색과 흰색으로 변환시켜 줍니다.
4. 이렇게 변환된 이미지 픽셀을 numpy로 저장하고 ravel()을 이용해 1차원으로 변형한 후 이 값을 X로 둡니다.
5. y_pred = mlp.predict(X)로 예측값인 y_pred를 확인하면 됩니다. 

OpenCV에 대한 자세한 내용은 제 블로그의 OpenCV 강좌를 참조하면 됩니다. 

이상으로 다층 퍼셉트론을 이용한 손글씨 숫자를 인식하는 내용은 마무리 하도록 하겠습니다.

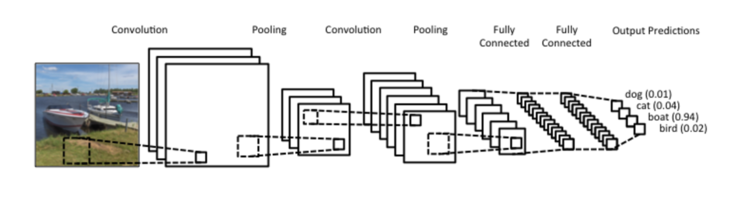
다음 포스팅에서는 구현한 역전파 알고리즘의 정확도를 체크하는 방법인 gradient checking에 대해 가볍게 살펴보도록 하고, 이후 포스팅부터는 또 다른 딥러닝 방법인 Convolutional Neural Network(CNN)과 Recurrent Neural Network(RNN)에 대한 내용을 다루도록 하겠습니다.

[35]편에서 역전파에 대한 개념적인 내용을 살펴보았습니다. 그런데, [35편]에서 역전파 개념을 설명할 때 도입한 비용함수 J(w)는 아래와 같이 오차제곱합으로 정의했습니다.

여기서 Φ(z)는 활성 함수인 시그모이드 함수값인거죠.

그리고 z는 각 층에서 순입력 함수값인거 아실겁니다.

그런데 활성함수가 시그모이드이고 오차제곱합으로 정의된 비용함수는 경사하강법을 적용하는데 약간의 문제가 있습니다. 오차제곱합으로 정의된 비용함수 J(w)를 그래프로 그려보면 아래와 비슷한 모양이 됩니다.

이런 모양을 이루고 있는 함수에서 경사하강법을 적용하게 되면 우리가 원하는 최소값에 도달하는 것이 아니라 아래 그림과 같이 국소적인 부분에서의 최소값에 도달하고 더 이상 진행할 수 없는 상태가 될 수 있습니다.

경사하강법이 성공적으로 적용되려면 볼록형태의 그래프를 가진 함수이어야 합니다. 그래서 머리 좋은 몇몇 사람들이 로지스틱 회귀를 위한 비용함수를 경사하강법이 적용될 수 있도록 그래프가 볼록한 모양으로 되는 새로운 비용함수를 아래와 같이 정의하게 됩니다.

하~ 복잡한 수식이네요.. 아무튼 위 식에서 n은 트레이닝 데이터의 개수이며, t는 출력층의 출력값의 개수입니다. 그리고 y는 트레이닝 데이터에 대한 실제값이며 a는 트레이닝 데이터에 대한 활성 함수값 즉 학습에 의한 결과값입니다.

그런데 이 수식은 복잡해보여도 트레이닝 데이터에 대한 실제 결과값 y의 값을 0 또는 1로 정의해버리면 단순하게 됩니다. y값이 1이면 J(w)의 두번째 항이 0으로 되고, y값이 0이면 J(w)의 첫번째 항이 0으로 됩니다. 즉,

​

​

이 두 개의 식을 하나로 표현한 것이 저 위에 있는 복잡해보이는 수식이 됩니다. 자, 이제 [35편]에서 언급한 가중치 업데이트 식을 다시 가져와 봅니다.

가중치 업데이트를 하려면 J에 대한 w의 미분값이 필요한거 이제 다 아는 이야기입니다. 위 J(w) 식에서 a는 시그모이드 함수 Φ(z)입니다. 시그모이드 함수 Φ를 미분하면 Φ(1-Φ)가 됩니다. 이 부분을 유념하면서 진행하도록 합니다.

[35편]에서 역전파 개념 이해를 위해 도입된 2-2-2 다층 퍼셉트론을 다시 불러옵니다.

여기서 순전파에 있어 값의 흐름을 다시 불러와서 적어보면 다음과 같습니다.

[식 1] 

그리고, 출력층 a1(3), a2(3)에서의 출력값과 실제값의 오차 J1, J2는 로지스틱 회귀의 비용함수를 이용해 다음과 같이 정의합니다.

[식2]

이제 [35편]에서 설명한 바와 마찬가지로 방법으로 역전파를 이용해 가중치를 업데이트 해보도록 합니다. 계산의 편의를 위해 learning rate η는 1로 둡니다.

먼저, w1,1(2)에 대한 업데이트 식을 구해봅니다. 이를 위해 Jtotal을 w1,1(2)에 대해 미분한 값을 구해야겠지요~ a1(3)에서 Jtotal은 J1이므로,

[식2]와 [식1]을 참조하여 위의 식을 계산하면 다음과 같습니다.

따라서

마찬가지로 Jtotal을 w1,2(2)에 대해서 미분한 값은 다음과 같습니다.

동일한 방법으로 가중치 w2,1(2), w2,2(2)에 대해서 계산해보면 다음과 같은 결과가 유도됩니다.

이 식들을 하나의 식으로 표현하면 다음과 같이 됩니다.

위 식을 아래와 같은 식으로 단순화하여 표현해봅니다.

[식3] 

여기서, j, k는 각각 은닉층의 출력값 개수 범위와 출력층의 출력값 개수 범위를 적용하면 되므로, 이로써 출력층에서 은닉층으로의 역전파에 대해 파이썬으로 구현하기 위한 알고리즘을 마련한 것 같습니다.

[35편]을 참조하여 은닉층에서 입력층으로의 역전파시 가중치 업데이트 식을 계산하여 정리하면 다음과 같습니다.

[식4]

여기서, i는 입력층의 입력값 개수가 범위이며, [식4]를 통해 은닉층에서 출력층으로의 역전파에 대해 파이썬으로 구현하기 위한 알고리즘도 마련되었습니다.

n1-n2-n3 다층 퍼셉트론에서 역전파시 가중치 업데이트를 위한 식은 아래와 같이 표현할 수 있습니다.

[식5]

이로써, 역전파를 통해 가중치를 업데이트하는 일반화된 식을 이용해 파이썬으로 잘 구현하면 될 것 같습니다.

실제로 다층 퍼셉트론을 코드로 구현할 때, 성능 향상을 위하여 비용함수에 정규화 L1, L2를 적용한 항을 추가하여 계산하게 됩니다.

여기서 잠깐..

[35편]과 [36편]에서 역전파를 이해하기 위해 도입한 활성함수는 시그모이드 함수입니다. 시그모이드 함수는 활성함수로서 여러가지 장점이 있는 함수임에는 틀림이 없으나 은닉층이 매우 많은 심층신경망에서는 단점이 존재하는데, 신경망의 은닉층이 많아질수록 역전파에 의한 가중치 보정이 의미가 없어지는 gradient vanishing 문제가 발생합니다.

gradient vanishing은 역전파를 수행하는 은닉층의 개수가 많아지면 J(w)의 w에 대한 편미분값이 0에 가까와져서 가중치 업데이트 식에 의한 가중치 갱신이 거의 이루어지지 않기 때문에 발생하는 현상입니다. 이는 [식5]의 δ의 절대값이 1보다 작기때문에 δ를 곱하면 곱할수록 0에 가까와지기 때문입니다.

gradient vanishing 현상을 해결하기 위해 새로운 활성함수를 도입하게 되는데 바로 ReLU(Rectified Linear Unit)라는 함수입니다. ReLU는 아래 그래프와 같이 입력값이 0보다 작거나 같으면 0, 0보다 크면 입력값을 리턴하는 함수입니다.

​

심층신경망에서 활성함수로써 ReLU는 시그모이드보다 훨씬 나은 성능을 보이며, 대부분의 심층신경망에서 활성함수로 널리 사용되고 있습니다.

따라서 [35편]과 [36편]에서 보인 시그모이드를 활성함수로 한 예시는 역전파의 개념을 이해하는데 만족하시고 실제 응용시에는 ReLU를 활성함수로 적용하면 됩니다.

다음 포스팅에서는 Sebstian Raschka의 책 "Python Machine Learning"에 있는 다층 퍼셉트론을 구현한 파이썬 코드를 소개하고, MNIST에서 제공하는 손글씨 숫자 이미지 60,000개를 이용해 MLP 딥러닝 학습을 수행한 후 손글씨 숫자 인식률에 대해서 살펴보도록 합니다. 

1958년 퍼셉트론이 발표된 후 같은 해 7월 8일자 뉴욕타임즈는 앞으로 조만간 걷고, 말하고 자아를 인식하는 단계에 이르는 컴퓨터 세상이 도래할 것이라는 다소 과격한 기사를 냈습니다.

​

하지만 1969년, 단순 퍼셉트론은 ​XOR 문제도 풀 수 없다는 사실을 MIT AI 랩 창시자인 Marvin Minsky 교수가 증명하였고, 다층 퍼셉트론(MLP)으로 신경망을 구성하면 XOR 문제를 풀 수 있으나, 이러한 MLP를 학습시키는 방법은 존재하지 않는다고 단정해버렸습니다.

이로 인해 떠들석했던 인공신경망과 관련된 학문과 기술은 더 이상 발전되지 않고 침체기를 겪게 됩니다.

그런데 1974년, 당시 하버드 대학교 박사과정이었던 Paul Werbos는 MLP를 학습시키는 방법을 찾게 되는데, 이 방법을 Minsky 교수에게 설명하지만 냉랭한 분위기속에 무시되버립니다.

​

Paul Werbos가 Minsky 교수에게 설명한 MLP를 학습시킬 수 있는 획기적인 방법이 바로 오류 역전파 (Backpropagation of errors)라는 개념입니다.

이제 오류 역전파(앞으로 그냥 역전파라고 부르겠습니다)가 무엇인지 살펴보도록 합니다.

​

심층 신경망을 학습한다는 것은 최종 출력값과 실제값의 오차가 최소가 되도록 심층 신경망을 이루는 각 층에서 입력되는 값에 곱해지는 가중치와 바이어스를 계산하여 결정하는 것을 말합니다.

우리는 [6편] 아달라인을 학습할 때 인공 신경망의 출력값과 실제값의 오차가 최소가 되도록 가중치를 결정하는 방법인 경사하강법에 대해 다룬적이 있습니다.

경사하강법은 오차 곡선을 따라 일정한 크기로 내려가면서 최소값을 찾아가는 방법인데, 일정한 크기는 해당 지점에서 접선의 기울기와 learning rate으로 결정한다고 했지요.

기억이 가물거리면 다시 [6편]을 학습하고 옵니다.

☞ 경사하강법 다시보러 가기

심층 신경망을 학습하는데 유용하게 활용되는 역전파(backpropagtion) 알고리즘도 결국 이 경사하강법을 이용합니다. 그러면 역전파가 무엇인지 그 개념에 대해 대충(?) 살펴보도록 합니다.

먼저 아래와 같은 2-2-2 다층 퍼셉트론이 있다고 생각해봅니다. 여기서는 역전파의 개념만 살펴볼 예정이므로 각 층에 존재하는 바이어스는 생략했습니다. 또한 용어의 통일성을 위해 입력층의 x1, x2는 a1(1), a2(1)로 표기하기로 합니다.

[34편]에서 l층의 i번째 노드와 l+1층의 j번째 노드를 연결하는 가중치 w를 다음과 같이 정의했지요~

이 구조에서 적용되는 활성 함수는 시그모이드 함수 φ입니다.

입력층 -> 은닉층 사이의 값의 흐름은 다음과 같습니다.

[식1] 

그리고 은닉층 -> 출력층 사이의 값의 흐름은 다음과 같습니다.

[식2] 

이와 같이 입력층의 a1(1), a2(1)을 시작으로 출력층의 a1(3), a2(3) 값이 출력되는 과정을 순전파(feedforward)라 부릅니다.

우리는 아달라인을 다룰 때 오차제곱합을 비용함수로 도입해서, 이 비용함수가 최소가 되도록 가중치를 결정했습니다. 물론 가중치를 결정하는 방법은 경사하강법이었죠.

여기서도 비용함수 J를 오차제곱합으로 정의를 해보면 다음과 같이 될 겁니다.

여기서 y1, y2는 트레이닝 데이터에 대한 각 노드에 대응되는 실제값입니다. 순전파 1회가 마무리되면 J1과 J2의 값이 결정되겠죠.

입력값 a1(1), a2(1)과 실제값 y1, y2는 고정된 값이므로 J1과 J2는 결국 가중치 w1,1(1)~w2,2(2)를 변수로 가지는 함수가 됩니다.

우리의 목표는 J1과 J2의 값이 최소가 되도록 w1,1(1)~w2,2(2)를 결정해야 합니다.

아달라인에서와 마찬가지로 다층 퍼셉트론에서도 비용함수의 최소값을 찾아가는 방법으로 경사하강법을 활용한다고 했습니다. 각 층에서 가중치를 업데이트하기 위해서는 결국 각 층에서의 비용함수(오차로 불러도 됩니다.)의 미분값이 필요하게 되는 것이지요.

이를 매우 효율적으로 해결하기 위한 방법이 바로 역전파 알고리즘입니다.

역전파란 역방향으로 오차를 전파시키면서 각층의 가중치를 업데이트하고 최적의 학습 결과를 찾아가는 방법입니다.

자, 이 경우를 한번 생각해봅니다.

순전파에 있어서 가중치의 값을 매우 미세하게 변화시키면 비용함수 J1, J2도 매우 미세하게 변화될 겁니다. 매우 미세하게 변화시킨다는 것은 미분을 한다는 이야기입니다. 그런데, 매우 미세한 영역으로 국한할 때 가중치의 미세변화와 이에 따른 비용함수의 미세변화가 선형적인 관계가 된다고 알려져 있습니다. 선형적인 관계라는 이야기는 결국 비용함수를 매우 미세하게 변화시키면 이에 따라 가중치도 매우 미세하게 변화되는데 이 역시 선형적인 관계라는 이야기입니다.

이런 원리에 의해, 순전파를 통해 출력층에서 계산된 오차 J1, J2의 각 가중치에 따른 미세변화를 입력층 방향으로 역전파시키면서 가중치를 업데이트하고, 또 다시 입력값을 이용해 순전파시켜 출력층에서 새로운 오차를 계산하고, 이 오차를 또다시 역전파시켜 가중치를 업데이트하는 식으로 반복합니다. 

역전파를 이용한 가중치 업데이트 절차는 아래와 같이 요약될 수 있습니다.

1. 주어진 가중치 값을 이용해 출력층의 출력값을 계산함(순전파를 통해 이루어짐)
2. 오차를 각 가중치로 미분한 값(실제로는 learning rate을 곱한 값)을 기존 가중치에서 빼줌(경사하강법을 적용하는 것이며, 역전파를 통해 이루어짐)
3. 2번 단계는 모든 가중치에 대해 이루어짐
4. 1~3단계를 주어진 학습회수만큼 또는 주어진 허용오차값에 도달할 때가지 반복함

2번 단계의 가중치 업데이트 식을 수식으로 표현하면 다음과 같습니다.

여기서 Jtotal은 해당 노드가 영향을 미치는 오차의 총합입니다. 예를 들면 출력층의 노드 a1(3)에서는 다른 노드의 오차에 영향을 전혀 미치지 않으므로 해당 노드에서 오차인 J1만 따지면 되지만, 은닉층의 a1(2) 노드는 출력층의 a1(3), a2(3) 노드의 오차에 영향을 미치므로 J1, J2 모두 더한 것이 Jtotal 값이 됩니다.

이번에는 역전파를 통한 가중치 업데이트 메커니즘을 살펴볼 것이므로 편의상 learning rate η는 1로 둡니다.

자, 그러면 실제로 역전파를 이용해 가중치를 업데이트 해보도록 하죠. 먼저 가중치 w1,1(2)에 대해서 계산을 해봅니다.

​

​

​

 w1,1(2)에 대한 업데이트 식은 아래와 같습니다.

미분의 연쇄법칙에 의해 오차의 가중치에 대한 미분값은 아래의 식으로 표현될 수 있습니다.

이제 위 식의 오른쪽 항에 있는 3개의 미분값을 하나하나 구해보도록 하지요~ 참고로 이 포스팅의 첫부분에서 서술한 순전파를 통한 값의 흐름을 요약한 수식을 참고하기 바랍니다.

역전파의 출발노드인 a1(3)에서 Jtotal의 값은 J1입니다. 따라서 위 식 오른쪽 항은 아래와 같이 계산됩니다.

따라서

역전파에서 가중치 업데이트를 위해 사용되는 오차의 가중치에 대한 미분값이 결국 역전파의 출발 노드의 활성 함수 값과 도착 노드의 활성 함수 값, 그리고 실제값만으로 표현되는 것을 알 수 있습니다.

​

​위 식의 오른쪽 항에서 처음 두 식의 값을 아래와 같이 δ1(3)으로 둡니다.

[식3]

역전파에 의해 업데이트 되는 w1,1(2)는 다음과 같습니다.

마찬가지 방법으로 w1,2(2)에 대한 업데이트 수식도 다음과 같습니다.

δ2(3)을 아래와 같은 수식으로 정의하고,

[식4]

w2,1(2), w2,2(2)에 대해서도 계산을 해보면

여기까지 서술해보니 뭔가 규칙성이 보입니다. 출력층에서 은닉층으로 역전파를 통해 전달되는 값이 결국 δ1(3) 과 δ2(3) 뿐이더라도 관련된 가중치를 업데이트하는데 충분하다는 것을 알 수 있습니다.

이제, 은닉층에서 입력층으로 향하는 역전파를 통해 w1,1(1)의 값을 업데이트 해보겠습니다.

w1,1(1)을 업데이트 하기 위해서 a1(2)에서 Jtotal을 w1,1(1)로 편미분한 값을 계산해야겠지요? 앞에서 적용한 것과 마찬가지로 미분의 연쇄법칙을 활용하면 다음과 같은 식이 됩니다.

위에서 언급했듯이 a1(2)에서 Jtotal은 J1과 J2를 더한 값이 됩니다. 따라서 위 식 오른쪽 항의 첫 번째 편미분값은 아래와 같이 계산됩니다. 

 그런데 출력층 -> 은닉층으로 역전파를 통한 가중치 계산시에 등장한 [식3]과 [식4]와 [식1], [식2]를 참고하여 계산해보면 다음과 같은 결과가 나옵니다.

가 됩니다.

나머지 편미분 값은 이미 해본 계산이므로 쉽게 계산됩니다.  w1,1(1)을 업데이트 하기 위한 편미분 값은 다음과 같습니다.

위 식의 오른쪽 항에서 처음 두 식을 δ1(2)로 둡니다. 

최종적으로 w1,1(1)의 업데이트 식은 아래와 같게 됩니다.

동일하게 w1,2(1)의 업데이트 식은 아래와 같습니다.

마찬가지로, δ2(2)를 다음과 같이 두고, 

w2,1(1), w2,2(2)에 대한 업데이트 식을 나타내면 다음과 같습니다.

따라서 모든 가중치에 대한 업데이트 식은 아래와 같이 표현할 수 있습니다.

여태까지 다룬 역전파 알고리즘 개념을 그림으로 도식화하여 나타내보면 다음과 같습니다.

이와 같이 순전파 -> 역전파 -> 가중치 업데이트 -> 순전파 .... 로 계속 반복해나가면 오차값이 0에 가까와지게 됩니다.  

이상으로 역전파 알고리즘 및 가중치 업데이트 원리를 살펴보았습니다. 역전파 알고리즘을 이해하기가 쬐금은 어렵지만, 이 부분이 딥러닝의 핵심적인 역할을 하는 부분이며, 완전한 이해가 힘들더라도 그 개념만이라도 알고 있으면 많은 도움이 됩니다.

[33편]까지 머신러닝의 기초적인 내용에 대해 거의 모두 다루었으므로, 이번 포스팅부터는 요즘 핫하게 뜨고 있는 딥러닝과 관련된 내용을 차근차근 다루어 보도록 하겠습니다.

먼저, [2편]에서 다루었던 인공신경망인 단층 퍼셉트론을 다시 상기해봅니다. 너무 오래된 일이라 기억이 나지 않으면 아래 링크를 눌러 살포시 다시 보고 옵니다.

☞ [2편] 퍼셉트론 다시 보러 가기

퍼셉트론의 활성 함수를 개선하여 퍼셉트론을 발전시킨 인공신경망이 아달라인이라고 했습니다. 아달라인은 [6편]에서 다루었는데, 이 역시 기억이 가물가물하다면 아래 링크를 눌러 다시 복습하고 옵니다.

☞ [6편] 아달라인 다시 보러 가기

이제, 퍼셉트론과 아달라인에 대해 다시 감을 잡았다고 생각하고, 포스팅을 진행하도록 하겠습니다.

[2편]과 [6편]에서 다룬 퍼셉트론과 아달라인은 데이터의 입력층과 출력층만 있는 구조입니다. 이러한 구조를 갖는 퍼셉트론을 단층 퍼셉트론이라 부른다고 했습니다.

퍼셉트론에서 결과값을 내놓는 부분은 결국 활성 함수(activation function)인데, 단층 퍼셉트론에서는 이 활성 함수가 1개밖에 없는 구조이지요. 위 그림에서 출력층의 활성 함수를 a로 표시했습니다.

인공신경망인 단층 퍼셉트론은 그 한계가 있는데, 비선형적으로 분리되는 데이터에 대해서는 제대로 된 학습이 불가능하다는 것입니다. 예를 들면 단층 퍼셉트론으로 AND연산에 대해서는 학습이 가능하지만, XOR에 대해서는 학습이 불가능하다는 것이 증명되었습니다.

이를 극복하기 위한 방안으로 입력층과 출력층 사이에 하나 이상의 중간층을 두어 비선형적으로 분리되는 데이터에 대해서도 학습이 가능하도록 다층 퍼셉트론(줄여서 MLP)이 고안되었습니다. 아래 그림은 다층 퍼셉트론의 구조의 한 예를 보인 것입니다.

입력층과 출력층 사이에 존재하는 중간층을 숨어 있는 층이라 해서 은닉층이라 부릅니다. 입력층과 출력층 사이에 여러개의 은닉층이 있는 인공 신경망을 심층 신경망(deep neural network)이라 부르며, 심층 신경망을 학습하기 위해 고안된 특별한 알고리즘들을 딥러닝(deep learning)이라 부릅니다.

따라서 딥러닝을 제대로 이해하기 위해서는 심층 신경망의 가장 기초적인 다층 퍼셉트론에 대해 제대로 알고 있어야 하겠지요~

​

다층 퍼셉토론에서는 입력층에서 전달되는 값이 은닉층의 모든 노드로 전달되며 은닉층의 모든 노드의 출력값 역시 출력층의 모든 노드로 전달됩니다. 이런 형식으로 값이 전달되는 것을 순전파(feedforward)라 합니다. 입력층과 은닉층에 있는 한개의 노드만 볼 때, 하나의 단층 퍼셉트론으로 생각할 수 있습니다. 따라서 은닉층에 있는 각각의 노드는 퍼셉트론의 활성 함수라고 볼 수 있습니다. 은닉층에 있는 각 노드에 이름을 a1~am으로 이름을 붙여서 그림을 그려보면 아래와 같겠지요.

마찬가지로 은닉층과 츨력층에 있는 한개의 노드만 고려해보면 이 역시 하나의 단층 퍼셉트론이며 출력층의 각 노드에 A1~A3로 이름을 붙여서 그림을 그려보면 아래와 같습니다.

은닉층과 출력층의 노드에 이름 붙여진 a1~am, A1~A3를 소문자 a로 통일되게 표현하기 위해 위첨자와 아래첨자를 도입해 봅니다. 입력층, 은닉층, 출력층은 각각 1번째, 2번째, 3번째 층이므로 a의 위첨자에 층을 표시하도록 해봅니다. 또한 은닉층에도 입력층에서와 같이 바이어스 a0를 추가하여 다층 퍼셉트론을 표현하면 아래 그림과 같이 됩니다.

위 그림에서 제시된 다층 퍼셉트론은 입력층의 노드수가 n개, 은닉층의 노드수가 m개, 출력층의 노드수가 3개입니다. 이렇게 구성되는 다층 퍼셉트론을 n-m-3 다층 퍼셉트론이라 부릅니다.

​

​단층 퍼셉트론과 마찬가지로 다층 퍼셉트론에서도 바이어스 x0, a0의 값은 보통 1로 두면 됩니다.

그러면 다층 퍼셉트론이 동작하는 원리에 대해 살펴봅니다.

우리는 단층 퍼셉트론이 동작하는 원리는 다 알고 있습니다. 단층 퍼셉트론은 활성 함수가 내놓는 결과값이 실제값과 오류가 최소가 되도록 입력층에서 전달되는 값들에 곱해지는 가중치의 값을 결정하는 것입니다.

다층 퍼셉트론의 동작 원리 역시 단층 퍼셉트론의 동작 원리와 크게 다를 것이 없습니다. 차이점은 단층 퍼셉트론은 활성 함수가 1개인 반면, 다층 퍼셉트론은 은닉층과 출력층에 존재하는 활성 함수가 여러개이고, 이에 따른 가중치도 여러개인 것이지요.

다층 퍼셉트론은 아래와 같이 동작합니다.

1. 각 층에서의 가중치를 임의의 값(보통 0으로 설정함)으로 설정합니다. 각 층에서 바이어스 값은 1로 설정합니다.
2.  하나의 트레이닝 데이터에 대해서 각 층에서의 순입력 함수값을 계산하고 최종적으로 활성 함수에 의한 출력값을 계산합니다.
3. 출력층의 활성 함수에 의한 결과값과 실제값이 허용 오차 이내가 되도록 각층에서의 가중치를 업데이트합니다.
4. 모든 트레이닝 데이터에 대해서 출력층의 활성 함수에 의한 결과값과 실제값이 허용 오차 이내가 되면 학습을 종료합니다.

그런데, 여기서 한가지 어려움이 있습니다. 단층 퍼셉트론에서는 은닉층이 존재하지 않고, 입력층과 출력층만 존재하기 때문에 출력층의 결과값을 우리가 확보한 실제값과 비교하여 오차가 최소가 되도록 가중치를 업데이트하고 결정하면 됩니다. 하지만 다층 퍼셉트론에서는 입력층과 출력층 사이에 은닉층이 존재하고, 은닉층의 출력값에 대한 기준값을 정의할 수 없습니다. 은닉층에서 어떤 값이 출력되어야 맞다 틀리다하는 기준이 없다는 것이지요.

이러한 문제점을 해결하기 위해 다층 퍼셉트론에서는 출력층에서 발생하는 오차값을 이용하여 은닉층으로 역전파(backpropagation)시켜 은닉층에서 발생하는 오차값에 따라 은닉층의 가중치를 업데이트하게 됩니다. 역전파에 대한 내용은 나중에 자세히 다루도록 하겠습니다.

다층 퍼셉트론의 동작 원리를 이해하기 위해 좀 더 구체적으로 들어가 보겠습니다.

l층의 k번째 노드와 l+1층의 j번째 노드를 연결하는 가중치 w를 다음과 같이 정의해봅니다.

자 다시, 위에서 제시한 n-m-3 다층 퍼셉트론에서 은닉층에 있는 j번째 노드를 생각해봅니다.

은닉층의 j번째 노드에 입력되는 순입력 함수값은 아래와 같습니다.

순입력 함수값은 해당 노드의 활성 함수에 입력되는 값입니다. 우리가 여태까지 배웠던 활성 함수를 되새겨 보면, 단순 퍼셉트론에서는 활성 함수로 계단 함수(step function)를, 아달라인에서는 1차 항등 함수를, 로지스틱 회귀에서는 시그모이드 함수를 적용했습니다.

​

다층 퍼셉트론의 활성 함수로 시그모이드 함수를 적용하게 되면 분석이 복잡해지긴 하지만 시그모이드 함수의 결과가 미분가능한 꼴이어서 역전파 알고리즘을 적용할 수 있게 되고, 나아가 이미지 분류 등과 같은 복잡한 비선형 문제를 풀 수 있는 잠재력을 지니게 됩니다.

여기서 잠깐~! 퍼셉트론의 활성 함수는 시그모이드가 아닌데.. 시그모이드를 활성 함수로 적용하게 되면 이는 로지스틱 회귀를 겹겹히 쌓아 놓은 구조가 되므로, 엄밀히 말하면 다층 퍼셉트론이라는 말은 좀 어폐가 있어 보이네요~ 아무튼 그냥 다층 퍼셉트론이라 부르기로 합니다.

시그모이드 함수에 대해서는 [12편]에서 다루었습니다. 아래 링크를 눌러서 살포시 학습하고 오시죠~

☞ 로지스틱 회귀 다시 보기

시그모이드 함수를 적용한 활성 함수를 φ라 하면 

따라서 은닉층의 j번째 노드의 활성 함수는 다음과 같이 표현할 수 있습니다.

이와 같이 각 층에서 순입력 함수값을 계산하고, 시그모이드 활성 함수에 의해 출력값을 계산하여, 최종적으로 출력층에서 활성 함수에 의한 결과값이 나오면 실제값과 오차를 계산한 후 가중치를 업데이트하는 행위를 반복하여 학습을 수행합니다.

학습의 결과가 허용된 오차 이내가 되면 각 층의 신경망에 곱해지는 가중치가 결정되는 것이고, 최종적으로 학습을 종료하게 됩니다. 이런 과정이 결국 딥러닝의 핵심 개념이라 보면 됩니다.

다층 퍼셉트론은 순전파(feedforward) 인공 신경망의 전형적인 예입니다. 순전파라는 말은 루프를 돌지 않으면서 각 층의 출력값이 그 다음층의 입력값이 된다는 의미입니다. 나중에 다룰 또 다른 인공 신경망인 RNN(Recurrent Neural Network)은 순전파와는 대비되는 개념이 적용됩니다.

단층 퍼셉트론과는 달리 다층 퍼셉트론의 출력층의 출력 노드는 여러개가 될 수 있습니다. 만약 3개 품종을 지닌 아이리스를 분류하는 다층 퍼셉트론은 출력층의 출력노드를 3개로 구성하고 그 결과값에 따라 품종 분류는 아래와 그림과 같은 형식으로 하면 될 것입니다.

출력층을 3개의 노드로 구성하고, 아이리스의 3개 품종 setosa, versicolor, verginica에 대한 실제값을 (1, 0, 0), (0, 1, 0), (0, 0, 1)로 정의합니다. 출력층의 1번째 노드 a1(3), 2번째 노드 a2(3), 3번째 노드 a3(3)의 값이 (1, 0, 0) 스러우면 아이리스 품종을 setosa로, (0, 1, 0) 스러우면 versicolor로 분류하는 식입니다.

​

활성 함수가 시그모이드 함수이므로 실제 출력층에서의 출력값은 0~1사이의 값을 갖게 됩니다. 따라서 출력값은 (0.9, 0.01, 0.19)과 같은 꼴로 될 것이며, 이는 (1, 0, 0) 스러우므로 setosa로 분류하면 됩니다. 

​

​만약 0~9까지 숫자를 인식하는 다층 퍼셉트론이라면 출력층의 노드 개수를 10개로 하면 될 것입니다. 

이정도로 다층 퍼셉트론에 대한 소개는 마무리 하도록 하겠습니다.

다음 포스팅에서는 심층 인공신경망 학습의 핵심인 역전파(backpropagation)에 대한 내용을 살펴보도록 하겠습니다. 

이번 포스팅에서는 밀도기반 클러스터링인 DBSCAN(Density-based Spatial Clustering of Applications with Noise)에 대해 살펴보고 클러스터링에 대한 내용을 마무리하도록 하겠습니다.

DBSCAN의 개념적 원리는 단순합니다. 이해를 위해 2차원 평면에 아래 그림과 같이 9개의 데이터가 분포되어 있다고 가정합니다.

여기에 반지름이 ε인 원이 있다고 하고, 1번 데이터부터 9번 데이터까지 원의 중심에 이 데이터들을 둔다고 생각해봅니다. 

1번 데이터를 반지름 ε인 원의 중심에 둔 그림입니다. 원안에 점이 1번을 제외하고는 없네요. 자 여기서 우리가 하나의 클러스터로 묶을 기준을 정의합니다. 이 원안에 적어도 4개 이상의 점들이 포함되는 녀석들만 골라서 하나의 클러스터로 분류하는 것으로 해보겠습니다. 위 그림처럼 1번 데이터를 원에 중심에 두었을 경우, 1번 데이터를 제외하고는 아무런 데이터가 없습니다. 이런 데이터들을 노이즈 데이터(noise point)라 부르며, 노이즈 데이터들은 클러스터에서 제외시킵니다.

위 그림에서 보는 바와 같이 3번 데이터를 원의 중심으로 두었을 때 4개의 점이 원안에 포함됩니다. 따라서 우리가 세운 기준에 충족하는 데이터가 됩니다. 이러한 데이터를 코어 데이터(core point)라 부릅니다. 코어 데이터들은 하나의 클러스터에 포함시킵니다.

​

그런데, 아래 그림에서 보는 것처럼 2번과 9번 데이터는 우리의 기준인 4개의 데이터를 포함하는 것에는 충족하지 못하지만 클러스터에 포함되는 코어 데이터인 3번 데이터를 포함하고 있습니다. 이런 데이터를 경계 데이터(border point)라 부르며 이 녀석들도 해당 클러스터에 포함시킵니다. 

이런 식으로 반지름 ε인 원을 이용해 코어 데이터, 경계 데이터, 노이즈 데이터들을 분류해보면 아래 그림과 같은 결과가 나옵니다.

위 그림은 최종적으로 데이터들을 분류한 것이며, 빨간색과 노란색 데이터들을 하나의 클러스터로 묶고, 회색 데이터는 클러스터에서 제외합니다.

DBSCAN의 원리는 이것이 다입니다.

자, 그러면 코드로 들어가 볼까요..

skl_dbscandata.py

이 코드는 필요한 모듈을 임포트한 후, 반달 모양으로 분포하는 샘플 데이터를 생성하고 화면에 출력합니다. 코드를 실행하면 아래와 같은 데이터 분포를 볼 수 있습니다.

샘플 데이터는 위쪽 반달 부분에 100개, 아래쪽 반들 부분에 100개의 데이터가 분포하고 있습니다.

이제 아래 코드와 같이 plotResult()라는 함수를 정의하고, k-means 클러스터링으로 샘플 데이터를 분류합니다. plotResult()는 다양한 클러스터링 기법으로 분류한 결과를 시각적으로 보이기 위한 것입니다.

skl_dbscandata.py에서 plt.scatter() 이하 2줄을 삭제하고 위 코드를 추가한 후 실행하면 아래와 같은 결과가 나옵니다.

k-means 클러스터링으로 분류한 결과는 어떤가요? 뭔가 제대로 분류된 것 같지가 않습니다. 아무래도 위쪽 반달과 아래쪽 반달로 구분해야 더 적절한것 같은데요.. 이제 32편에서 다루었던 응집형 계층적 클러스터링으로 한번 분류해보죠.

기존 코드에 아래의 코드를 추가합니다.

계층적 클러스터링의 결과도 k-means와 비슷하지만 그래도 좀 품질이 좋아진 것 같네요. 이제 이번 포스팅의 주제인 DBSCAN을 이용해 분류해봅니다. 기존 코드에 아래의 코드를 추가합니다.

코드에서 DBSCAN의 인자 eps가 위에서 언급했던 원의 반지름이며, min_samples는 원에 포함되는 데이터 개수의 최소값입니다. 추가한 코드를 실행하면 아래와 같은 결과가 나옵니다.

드디어 우리가 원하던 결과가 나온 것 같습니다.

우리가 여태 다루었던 k-means 클러스터링, 계층적 클러스터링, DBSCAN은 데이터 간 유사도를 위해 유클리드 거리를 적용하여 계산했습니다. 유클리드 거리를 이용하는 기법에는 '차원의 저주(curse of dimensionality)'라는 효과가 발생한다는 단점이 존재합니다.

차원의 저주는 머신러닝, 데이터 마이닝 분야에서 사용하는 용어인데 데이터의 차원이 증가하면 해당 공간의 부피가 기하급수적으로 증가하게 되고, 모델을 추정하기 위해 필요한 샘플 데이터의 개수도 기하급수적으로 증가합니다. 또한 공간 상에 분포하는 데이터의 밀도 역시 매우 희박하게 됩니다. 이런 현상을 차원의 저주라는 표현을 써서 어려움을 나타내는 것이지요.

아무튼 DBSCAN에서 차원의 저주를 극복하기 위해 적절한 ε의 값과 최소 샘플 데이터 개수를 정하는 것이 중요한 포인트입니다.

이로써 머신러닝 기초에 대한 개념과 원리, 내용에 대해서는 거의 다 살펴본 것 같습니다. 앞으로의 포스팅에서는 요즘 핫하게 뜨고 있는 딥러닝을 이해하기 위한 인공신경망에 대해 본격적으로 공부해 보기로 합니다. 

데이터 분포를 그래프로 표현하면 데이터가 몇개의 그룹으로 분류될 수 있는지 눈으로 확인할 수 있습니다. 그런데, 컴퓨터의 입장에서는 몇 개의 그룹으로 데이터를 분류해야 최적의 결과가 되는지 알기가 어렵습니다. 데이터가 산만하게 분포되어 있는 경우, 사람의 눈으로도 2개로 나누어야 할지, 3개로 나누어야 할지 모호할 때가 있습니다. 

이번 포스팅에서는 k-means 클러스터링으로 데이터를 분류하고자 할 때, 최적의 클러스터 개수를 결정하는 방법에 대해 살펴봅니다.

최적의 클러스터 개수를 결정하는데 사용되는 대표적인 방법은 다음과 같은 2가지가 있습니다.

• 엘보우(elbow) 기법
• 실루엣(silhouette) 기법

엘보우 기법

[30편]에서 k-means 클러스터링은 클러스터내 오차제곱합(SSE)의 값이 최소가 되도록 클러스터의 중심을 결정해나가는 방법이라고 했습니다. 만약 클러스터의 개수를 1로 두고 계산한 SSE 값과, 클러스터의 개수를 2로 두고 계산한 SSE 값을 비교했을 때, 클러스터의 개수를 2로 두고 계산한 SSE 값이 더 작다면, 1개의 클러스터보다 2개의 클러스터가 더 적합하다는 것을 짐작할 수 있습니다.

이런 식으로 클러스터의 개수를 늘려나가면서 계산한 SSE를 그래프로 그려봅니다. SSE의 값이 점점 줄어들다가 어느 순간 줄어드는 비율이 급격하게 작아지는 부분이 생기는데, 그래프 모양을 보면 팔꿈치에 해당하는 바로 그 부분이 우리가 구하려는 최적의 클러스터 개수가 됩니다. elbow가 우리말로 팔꿈치라는거 다 아실거고요~

[30편] skl_clusterdata.py 맨 아래에 다음 코드를 추가합니다.

elbow(X)는 클러스터 개수에 따른 데이터 X의 SSE 값을 그래프로 그려주는 함수입니다. 코드에서 km.inertia_가 k-means 클러스터링으로 계산된 SSE 값입니다.

위 코드를 추가한 코드를 실행하면 다음과 같은 그래프가 화면에 출력됩니다.

위 그래프를 보면 클러스터의 개수가 3일 때 팔꿈치 부분이라는 것을 알 수 있습니다. 따라서 주어진 데이터를 구분하기 위한 최적의 클러스터의 개수는 3개로 결정하면 됩니다.

실루엣 기법

실루엣 기법은 클러스터링의 품질을 정량적으로 계산해주는 방법입니다. i번째 데이터 x(i)에 대한 실루엣 계수 s(i) 값은 아래의 식으로 정의됩니다.

여기서 a(i)는 클러스터내 데이터 응집도(cohesion)를 나타내는 값으로, 데이터 x(i)와 동일한 클러스터내의 나머지 데이터들과의 평균 거리입니다. 이 거리가 작으면 응집도가 높겠지요.

b(i)는 클러스터간 분리도(separation)를 나타내는 값으로, 데이터 x(i)와 가장 가까운 클러스터내의 모든 데이터들과의 평균거리입니다.

만약 클러스터 개수가 최적화 되어 있다면 b(i)의 값은 크고, a(i)의 값은 작아집니다. 따라서 s(i)의 값은 1에 가까운 숫자가 됩니다. 반대로 클러스터내 데이터 응집도와 클러스터간 분리도의 값이 같으면 실루엣 계수 s(i)는 0이 됩니다. 즉 실루엣 계수가 0이라는 것은 데이터들을 클러스터로 분리하는 것이 무의미하다는 것이겠지요.

아무튼 클러스터의 개수가 최적화되어 있으면 실루엣 계수의 값은 1에 가까운 값이 됩니다.

아래의 코드를 봅니다.

skl_silhouette.py

이 코드에서 plotSilhouette(X, y_km)은 데이터 X와 X를 임의의 클러스터 개수로 계산한 k-means 결과인 y_km을 인자로 받아 각 클러스터에 속하는 개별 데이터의 실루엣 계수값을 수평 막대그래프로 그려주는 함수입니다.

>>> cluster_labels = np.unique(y_km)

y_km의 고유값을 멤버로 하는 numpy 배열을 cluster_labels로 둡니다. y_km의 고유값 개수는 클러스터의 개수와 동일합니다.

>>> n_clusters = cluster_labels.shape[0] 

클러스터 개수를 n_clusters로 둡니다.

>>> silhouette_vals = silhouette_samples(X, y_km, metric='euclidean')

실루엣 계수를 계산하고 그 결과를 silhouette_vals로 둡니다.

plotSilhouette()의 for 구문은 각 클러스터에 속하는 데이터들에 대한 실루엣 값을 수평 막대그래프로 그려주는 로직입니다. 클러스터를 구분하기 위해 matplotlib.cm에서 제공하는 컬러맵 중 JET를 이용해서 칠해줍니다.

참고로 JET 컬러맵은 아래와 같습니다.

왼쪽 파란색 부분은 0.0, 오른쪽 빨간색 부분은 1.0 값을 가집니다. 중간 부분의 색상을 선택하려면 0과 1사이의 실수를 정해주면 됩니다.

>>> silhoutte_avg = np.mean(silhouette_vals)

>>> plt.axvline(silhoutte_avg, color='red', linestyle='--')

모든 데이터들의 실루엣 계수의 평균값을 빨간 점선으로 표시합니다.

skl_silhouette.py는 [30편]에서 다루었던 150개의 샘플 데이터를 3개의 클러스터로 나누어 k-means 클러스터링을 수행하고, 실루엣 계수를 그래프로 그려주는 코드입니다.

코드를 실행하면 아래와 같은 결과가 화면에 나옵니다.

클러스터 1~3에 속하는 데이터들의 실루엣 계수가 0으로 된 값이 아무것도 없으며 실루엣 계수의 평균이 0.7보다 크므로 잘 분류된 결과라 해도 무방합니다.

skl_silhouette.py에서 아래의 코드를 찾아 인자 n_clusters의 값을 2로 수정해봅니다.

>>> km = KMeans(n_clusters=2, random_state=0)

수정한 코드를 실행하면 다음과 같은 결과가 화면에 나타납니다.

클러스터1은 실루엣 계수의 값이 비교적 좋은 편이지만, 클러스터2는 실루엣 계수가 0인 것들도 있고 전체적으로 값이 0.6이하로 품질이 좋지 않음을 알 수 있습니다.

실제 데이터를 분류한 k-means 클러스터링 결과는 아래와 같게 나옵니다.

당연히 클러스터 3개로 구분했을 때보다 품질이 좋지 않다는 것을 알 수 있습니다.

엘보우 기법은 k-means 클러스터링에만 유효하지만, 실루엣 기법은 k-means 클러스터링 이외의 다른 클러스터링에도 적용할 수 있는 기법입니다.

이제 클러스터링에 있어 최적의 결과를 보이는 클러스터의 개수를 구하는 방법에 대해 배웠으니 실무에 잘 응용하시면 되겠습니다. 

우리는 여태까지 답이 이미 제시되어 있는 데이터를 이용하여 학습을 수행하고, 알려져 있지 않은 데이터에 대해 예측을 하는 지도학습(supervised learning) 유형의 머신러닝에 관해 살펴보았습니다.

이제 머신러닝의 또 다른 방법인 비지도학습(unsupervised learning)에 대해 다루어보도록 합니다.

다양한 자동차 그림을 제시하고 버스, 트럭, 승용차를 구분하는 경우를 생각해봅니다. 제시한 그림에는 자동차의 그림만 있을 뿐이며, 각 그림에는 자동차 종류를 표시한 어떠한 글자도 답도 태그도 없습니다. 따라서 이런 유형의 분류 문제는 비지도학습의 한 예가 될 것입니다.

아래와 같은 150개의 데이터 분포가 있다고 가정합니다.

위 그림을 보면 데이터가 3개의 그룹으로 나누어져 있다고 생각할 수 있습니다. 데이터에는 좌표만 있을 뿐 각 데이터를 구분할 수 있는 답이나 태그가 없습니다. 앞에서 말한 자동차 그림을 제시하고 버스, 트럭, 승용차로 구분하라고 한 경우, 버스와 트럭, 승용차의 특성들을 고려하여 좌표상에 찍어보면 아마도 위와 비슷하게 3개의 그룹으로 분리되어 표시될 수도 있을 겁니다.

이런 유형의 문제를 해결하기 위해 가장 대중적으로 사용되는 방법이 클러스터링(clustering), 우리말로 군집화라고 하는 알고리즘입니다. 클러스터링은 특성이 비슷한 개체들을 하나의 그룹으로 구분해 주는 기법입니다.

클러스터링은 다음과 같은 4가지 유형으로 구분됩니다.

• 클러스터 중심(centroid) 또는 평균 기반 클러스터링 k-means
• 빈도수가 많은 중간점(medoid) 기반 클러스터링 k-medoids
• 밀도 기반 클러스터링
• 계층적(hierarchical) 클러스터링

이번 포스팅에서는 k-means 클러스터링(우리말로 k-평균 군집화)에 대해 살펴봅니다.

k-means 클러스터링에서 k는 구분하고자 하는 클러스터(그룹)의 개수를 의미합니다. 위에서 제시된 그림처럼 3개의 클러스터로 분리되어 있는 경우 k는 3이 될 것입니다.

k-means 클러스터링 알고리즘이 동작하는 원리는 의외로 단순하며 주어진 데이터를 구분하기 위한 단계는 아래와 같습니다.

• 1단계: 
  • 클러스터의 개수 k값을 선택합니다. 위 그림과 같은 경우 k=3으로 두어야 하겠지요.
  • 데이터가 분포된 공간상에 클러스터 중심으로 가정할 임의의 지점을 k개 선택합니다.
• 2단계: 
  • 임의로 선택한 k개의 클러스터의 중심과 개별 데이터 사이의 거리를 계산합니다.
  • 개별 데이터는 가장 가깝게 있는 클러스터의 중심을 그 데이터가 소속되는 클러스터로 할당합니다.
• 3단계:
• 클러스터에 속하게 된 데이터들의 평균값을 새로운 클러스터의 중심으로 둡니다.
• 4단계
• 2~3단계를 알고리즘이 수렴할 때까지 반복합니다. 수렴한다는 의미는 클러스터의 중심이 더 이상 변화가 없게 된다는 말입니다.

​2단계에서 언급한 거리(distance)는 유클리드 거리의 제곱을 말하며, 특성이 m개인 두 데이터 x, y의 유클리드 거리 제곱은 다음과 같이 정의됩니다.

​

N개의 데이터가 있고, 이를 K개의 클러스터로 분류한다고 하면, k-means 클러스터링은 아래 J값이 최소가 되도록 w(i, k)와 μ(k)를 결정하는 것입니다.

​

이 식에서 x(i)는 i번째 데이터, μ(k)는 k번째 클러스터의 중심이며, w(i, k)는 x(i)가 k번째 클러스터에 속하는 경우 1, 그렇지 않은 경우 0으로 정의되는 값입니다.

J를 클러스터내 오차제곱합 또는 왜곡값(distortion)이라 부르기도 하고 클러스터 관성값(cluster inertia)이라 부르기도 합니다.

이정도로 k-means 클러스터링의 내부적인 처리에 대해서는 마무리하도록 합니다.

​

k-means 클러스터링의 동작 방식에 대한 이해를 돕기 위해 아래의 그림을 보시죠~

위 그림은 k-means 클러스터링으로 3개의 그룹(k=3)으로 구분하는 메커니즘을 보인 것입니다.

iteration1에서 임의의 3개의 지점(십자가 표시)을 정하고 이를 각 클러스터의 중심으로 가정한 후, 각 데이터는 가장 가깝게 위치하는 중심에 해당하는 클러스터로 편입시킵니다. iteration1 그림에서 초록색으로 표시된 데이터는 맨 왼쪽 십자가가 가장 가까운 중심이며, 빨간색으로 표시된 데이터들은 위쪽 십자가, 파란색으로 표시된 데이터들은 맨 오른쪽 십자가 가장 가까운 중심입니다.

​ 

iteration2에서는 iteration1에서 분류된 각 색상별 점들의 평균값을 새로운 클러스터의 중심으로 정하고, 개별 데이터들과의 거리를 다시 계산한 후 새로운 클러스터로 구분합니다. 이런 식으로 알고리즘을 반복해서 클러스터의 중심이 변하지 않으면 알고리즘을 종료합니다. iteration5와 iteration6 그림을 보면 클러스터의 중심이 변하지 않았음을 볼 수 있습니다.

k-means 클러스터링 알고리즘은 초기에 선택하는 임의의 클러스터 중심의 위치에 따라 클러스터링의 성능과 품질에 영향을 많이 받습니다. k-means++ 알고리즘은 최초 클러스터의 중심을 임의로 선택하는 것이 아니라 특정 알고리즘에 의해 선택하여 k-means 클러스터링의 성능과 품질을 좋게 해줍니다.

k-means++에 대한 자세한 내용은 생략합니다.

이제 scikit-learn이 제공하는 k-means 클러스터링 API를 이용해서 코드를 구현해보도록 합니다. 아래의 코드를 봅니다.

skl_clusterdata.py

이 코드는 150개의 샘플 데이터를 3개의 클러스터로 구분하여 분포하도록 만들어줍니다. 코드를 실행하면 다음과 같은 결과가 나오게 됩니다.

skl_clusterdata.py 맨 아래 부분에 다음의 코드를 추가합니다.

코드에서 init_centroid는 k-means 클러스터링의 초기 클러스터 중심을 선택하는 방법을 지정해주는 변수로 정의했습니다. 이 값이 'random'이면 초기 클러스터의 중심을 임의로 선택하라는 의미이며, 이 값이 'k-means++'이면 초기 클러스터의 중심을 k-means++를 이용해 선택하라는 의미입니다. 따라서 주석을 적절하게 변경하여 'random'이나 'k-means++'로 지정하면 됩니다.

>>> km = KMeans(n_cluster=3, init=init_centroid, random_state=0)

KMeans는 scikit-learn이 제공하는 k-means 클러스터링 API입니다. 각 인자의 의미는 다음과 같습니다.

• n_cluster: 클러스터의 개수 k 값을 지정합니다.
• init: 초기 클러스터 중심을 선택하는 방법을 지정합니다. 디폴트는 k-means++

>>> y_km = km.fit_predict(X)

k-means 클러스터링으로 구분한 결과를 y_km으로 얻습니다. y_km은 각 데이터가 속하는 클러스터를 나타내는 인덱스로 구성된 numpy 배열입니다. 우리가 지정한 클러스터는 3개이므로 인덱스는 0, 1, 2중 하나가 될 것입니다. 만약 y_km의 값이 [0 1 2 0 0 1 .... ] 이라고 가정하면 1번째 데이터는 클러스터0, 2번째 데이터는 클러스터1, 3번째 데이터는 클러스터2, 4번째 데이터는 클러스터0, ... 이라는 의미입니다.

코드를 실행하면 아래와 같은 결과가 나옵니다.

3개의 그룹으로 분포된 데이터를 k-means 클러스터링으로 잘 구분해주었음을 알 수 있습니다. 

우리는 의사결정트리 학습과 랜덤 포레스트를 이용해 데이터를 학습하고 분류하는 것에 대해 공부한 적이 있습니다. 기억나지 않는다면 아래의 링크를 살포시 눌러서 가볍게 훝어보고 옵니다.

​

☞ 의사결정트리 학습 바로가기

☞ 랜덤 포레스트 바로가기

회귀 분석에 있어서도 의사결정트리를 이용하거나 랜덤 포레스트를 이용해서 회귀 모델을 구할 수 있습니다. 단 차이점은 분류를 위한 의사결정트리 학습과 랜덤 포레스트에서는 정보이득의 불순도 측정을 위해 지니 인덱스나 엔트로피를 사용했다면, 회귀 모델을 위한 정보이득의 불순도 측정은 평균 제곱 오차 MSE로 한다는 것입니다.

개념은 이전에 학습했던 것과 동일하므로 바로 코드로 들어가 보죠~

skl_DTRegression.py

>>> rm = DecisionTreeRegressor(max_depth=3)

의사결정트리 회귀를 위해 scikit-learn의 DecisionTreeRegressor 객체를 이용합니다. 이 객체의 인자 max_depth의 값을 적절하게 조절하여 언더피팅이나 오버피팅이 되지 않도록 하는 것이 중요합니다.

>>> sort_idx = X.ravel().argsort()

의사결정트리 회귀의 결과를 그래프로 표시하기 위해 X의 요소값이 작은 순서로 정렬한 인덱스를 sort_idx로 둡니다. 말이 어려운데, 예를 들어 [1, 0, 5].argsort()의 값은 [1, 0, 2]가 됩니다.

결정 계수의 값을 계산하고 결과를 화면에 출력하면 다음과 같습니다.

결정 계수의 값이 0.70으로 제법 훌륭한 결과가 나옵니다.

이제 랜덤 포레스트를 활용하여 회귀 모델을 구하는 것을 해보도록 합니다. skl_DTRegression.py에서 아래의 모듈을 임포트합니다.

>>> from sklearn.ensemble import RandomForestRegressor

rm = DecisionTreeRegressor(max_depth=3)을 아래의 코드로 변경합니다.

>>> rm = RandomForestRegressor(n_estimators=1000, criterion='mse',

                                                  random_state=1, n_jobs=-1)

수정한 코드를 실행하면 아래와 같은 결과가 나옵니다.

결정 계수의 값은 0.91로 매우 훌륭한 결과가 나옵니다만, 회귀 모델 그래프를 보니 뭔가 오버피팅 되어 있다는 느낌이 강합니다. 샘플 데이터를 트레이닝 데이터와 테스트 데이터로 나누어서 측정해봐야 겠습니다.

skl_DTRegression.py에서 rm = DecisionTreeRegressor(max_depth=3) 이하를 모두 지우고, 아래의 코드를 추가합니다.

위 코드를 적용한 skl_DTRegression.py를 실행하면 다음과 같은 결과가 나옵니다.

샘플 데이터의 70%를 트레이닝 데이터로 해서 랜덤 포레스트로 계산한 회귀 모델의 결정 계수는 0.921로 매우 높지만, 테스트 데이터를 적용하면 결정 계수의 값이 0.544로 뚝 떨어집니다. 따라서 이 데이터 모델에 대한 랜덤 포레스트 회귀 모델은 오버피팅이 강하게 되어 있다는 것을 알 수 있습니다.

데이터 모델에 따라서 랜덤 포레스트의 결과가 오버피팅이 되어 있을 지라도 테스트 데이터에 대한 결정 계수가 높게 나온다면 바람직한 모델을 구한 것이 됩니다. 아래의 코드를 skl_DTRegression.py에 맨 아래에 추가합니다.

이 코드는 '회귀 분석 - 회귀 모델의 적합도 측정' 포스팅에서 잔차 분석을 위해 사용된 MEDV와 나머지 주택 정보들에 대해, 랜덤 포레스트로 회귀 모델을 구하고 트레이닝 데이터 및 테스트 데이터의 결정 계수를 계산하는 코드입니다.

코드를 수행하면 아래와 같은 결과가 나옵니다.

R2 - Train: 0.980, Test: 0.910

결과를 보면 트레이닝 데이터의 결정 계수에 비해 테스트 데이터의 결정 계수가 작지만 그 값이 0.910으로 적합도가 매우 훌륭하게 나온다는 것을 알 수 있습니다.

이로써 회귀 분석에 대한 내용은 모두 마무리 하도록 하겠습니다.

분석하고자 하는 데이터의 설명변수와 응답변수가 선형적인 관계가 아니라 곡선 형태로 되어 있는 경우, 선형 회귀 모델을 이용해 계산하게 되면 오차가 크게 나타날 것입니다.

만약 분석하고자 하는 데이터 분포가 2차원 곡선 형태로 되어 있으면 2차원 곡선으로, 3차원 곡선 형태로 되어 있으면 3차원 곡선으로 접근하는 것이 오차가 작겠지요.

아래와 같은 데이터 분포를 봅니다.

위 그래프와 같은 데이터 분포는 위로 볼록한 2차원 곡선 형태로 되어 있다고 말할 수 있겠지요. 이런 경우, 우리가 구하고자 하는 회귀 모델 식은 아래의 식과 같이 가정할 수 있습니다.

동일한 개념으로 일반적인 곡선에 대해 회귀 모델을 가정하면 아래와 같이 표현할 수 있겠습니다.

따라서 위 그래프는 d=2 로 두고 회귀 모델을 구하는 것이라고 보면 됩니다.

회귀 모델식을 위와 같이 다차원 다항식으로 두고 회귀 분석을 수행하는 것을 다항 회귀(Polynomial Regression)라 합니다. 그런데 이 다항 회귀도 결국 다중 회귀식의 일종임을 알 수 있습니다. 앞서 말했듯이 다중 회귀는 설명 변수가 여러 개 있는 식에서 설명 변수 계수를 구하는 것이라 했습니다. ​아래의 치환식을 생각해봅니다.

​

이 치환식을 적용하면 위에서 보인 다항 회귀 모델식은 아래와 같은 식으로 표현할 수 있습니다.

즉, 다항 회귀 모델은 다중 회귀 모델로 계산될 수 있다는 말입니다.

코드를 보면서 이해해 보도록 합니다. 먼저 아래와 같이 필요한 모듈을 임포트합니다.

위 코드 아래에 다음 코드를 추가합니다.

skl_polyregression.py

이 코드에서 X와 y는 이 포스팅 처음에 보인 그래프에서 데이터의 분포와 같은 값을 가집니다. 다항 회귀를 적용하려면 아래와 같은 순서로 로직을 구현합니다.

1. 다항 회귀를 위한 필요한 차수만큼 항을 추가하기 위해 PolynomialFeatures() 객체를 생성합니다.
2. 트레이닝 데이터 X를 PolynomialFeatures.fit_transform(X)로 변형합니다.
3. LinearRegression.fit()에 2단계의 결과를 적용하여 회귀 모델을 구합니다.

그러면 코드를 보시죠~

>>> lr = LinearRegression()

>>> pr = LinearRegression()

lr은 단순 선형 회귀 모델로 계산하기 위한 것이고, pr은 다항 회귀를 적용하여 다중 회귀 모델로 계산하기 위한 것입니다. 따라서 pr이 우리가 주목해야 할 부분입니다.

>>> quadratic = PolynomialFeatures(degree=2)

다항 회귀를 위해 2차항을 적용합니다.

>>> X_quad = quadratic.fit_transform(X)

트레이닝 데이터 X를 2차항이 적용된 다항 회귀 모델로 변형합니다.

>>> pr.fit(X_quad, y)

다항 회귀를 위해 변형된 트레이닝 데이터 X_quad를 이용해 회귀 모델 pr을 계산합니다.

>>> y_quad_fit = pr.predict(quadratic.fit_transform(X_fit))

계산된 회귀 모델로 좌표값 X_fit의 예측값을 계산합니다. 계산한 (X_fit, y_quad_fit)을 그래프에 그려주면 회귀 모델 그래프가 그려집니다.

나머지 코드는 회귀 모델 그래프를 화면에 그려주고, 단순 선형 모델의 MSE와 결정 계수값, 다항 회귀 모델을 적용하여 계산한 회귀 모델의 MSE와 결정 계수값을 보여주는 코드입니다.

코드를 실행하면 다음과 같은 결과가 나옵니다.

​

그래프를 보면, 단순 회귀 모델로 계산된 것은 점선으로 된 직선이고, 다항 회귀를 적용한 회귀 모델은 초록색 곡선입니다. 또한 단순 회귀 모델에 의해 계산된 MSE는 569.78로 다소 크지만 다항 회귀를 적용한 다중 회귀 모델의 MSE는 61.33으로 많이 줄어들었음을 알 수 있습니다. 또한 결정 계수의 값도 0.83에서 0.98로 1에 더욱 가까와져 적합도가 더욱 좋아졌습니다.

그러면 여태 다루었던 주택 정보에 다항 회귀를 적용해 보도록 하겠습니다. '회귀 분석 - 준비하기'에서 보인 페어플롯을 다시 보도록 합니다.

페어플롯에서 MEDV-LSTAT에 해당하는 그래프를 보면 데이터가 2차원 곡선 형태 비스므리하게 분포되어 있음을 알 수 있습니다.

skl_polyregression.py를 아래의 코드로 수정합니다.

skl_polyregression1.py

이 코드는 3차 다항 회귀 모델을 적용하는 부분이 추가된 것 말고는 전체적인 로직이 skl_polyregression.py와 동일합니다. 코드를 실행하면 아래와 같은 결과가 나옵니다.

각 회귀 모델의 결정 계수를 보면 결과가 썩 훌륭하지는 못합니다. 모든 비선형 모델에 다항 회귀 모델을 적용하는 것이 팔방미인은 아닙니다. 가끔은 데이터를 다른 식으로 변형해서 단순 회귀 모델로 계산할 때 더 좋은 결과를 보일 때도 있습니다. 이는 데이터를 바라보고 분석하는 사용자의 직관이나 경험이 중요하다는 것을 말해 줍니다.

MEDV-LSTAT 데이터에서, MEDV는 로그 값을 취하고, LSTAT은 제곱근 값을 취한 후, 단순 회귀 모델로 계산해보는 코드는 아래와 같습니다.

skl_polyregression1.py의 #그래프 그리기 부분을 삭제하고  이 코드를 추가합니다. 수정한 코드를 실행하면 다음과 같은 결과가 나옵니다.

결정 계수 값이 0.69로 이전의 결과보다 더 나아졌다는 것을 알 수 있습니다.

이는 데이터의 분포 형태에 따라 단순 회귀 모델로 계산할지, 다항 회귀를 적용한 다중 회귀 모델로 계산해야 할지 결정하는 것도 중요하지만, 데이터를 바라보고 직관적으로 해석하는 사용자의 경험이나 능력도 중요하다는 것을 말해줍니다.

우리는 로지스틱 회귀를 공부할 때, 머신러닝을 통해 획득한 모델이 오버피팅 또는 언더피팅이 되지 않도록 하기 위해 사용되는 기법인 정규화에 대해 살펴본 적이 있습니다. 물론 기억이 가물가물 하겠지요~ 아래의 링크를 살포시 눌러 기억을 되살리고 옵니다~

​

☞ 로지스틱 회귀 살펴보러 가기

회귀 분석에서도 정규화를 적용하여 회귀 모델을 계산하게 되면 최적의 모델을 구하는데 도움이 됩니다.

정규화를 적용하여 회귀 분석을 수행하는 방법은 아래와 같이 3가지가 있습니다.

• 리지 회귀(Ridge Regression)
• L2 정규화 적용 모델
• 라쏘(LASSO; Least Absolute Shrinkage and Selection Operator)
• L2 정규화 보다 약한 모델
• Elastic Net
• L2와 LASSO를 조합한 모델

위 3가지 정규화 방법에 따라 회귀 모델을 구하기 위해 사용되는 비용함수 J(w)는 다음과 같습니다.

리지 회귀를 위한 비용함수

라쏘를 위한 비용함수

Elastic Net을 위한 비용함수

바로 직전 포스팅의 skl_ra.py에 필요한 모듈을 추가하고 lr = LinearRegression() 부분 다음에 아래 코드와 같이 Ridge(), LASSO(), ElasticNet() 을 추가합니다.

skl_ra1.py

먼저 위 코드와 같이 skl_ra1.py에서 lr = Ridge() 부분만 주석을 해제하고 나머지 호출 부분은 주석 처리해줍니다.

>>> lr = Ridge(alpha=1.0)

Ridge()의 인자 alpha는 위에서 보인 수식의 λ와 비슷한 역할을 합니다. 이 값을 1.0으로 설정합니다.

>>> lr = ElasticNet(alpha=1.0, l1_ratio=0.5)

ElasticNet()인자 l1_ratio는 Elastic Net을 위한 cost function 식에서 λ2 의 비율을 뜻합니다. 이 값을 1.0으로 설정하면 LASSO와 동일한 효과를 갖습니다.

이 코드에 바로 앞 포스팅에서 적용한 MSE, 결정 계수를 계산해주는 코드를 추가하여 실행하면 다음과 같은 결과가 나옵니다.

MSE - 트레이닝 데이터: 20.14, 테스트 데이터: 27.76
R2 - 트레이닝 데이터: 0.76, 테스트 데이터: 0.67

주석을 순차적으로 변경하여 코드를 수행하여 결과를 정리하면 다음과 같습니다.

LinearRegression 적용

MSE - 트레이닝 데이터: 19.96, 테스트 데이터: 27.20
R2 - 트레이닝 데이터: 0.76, 테스트 데이터: 0.67

Ridge 적용

MSE - 트레이닝 데이터: 20.14, 테스트 데이터: 27.76
R2 - 트레이닝 데이터: 0.76, 테스트 데이터: 0.67

LASSO 적용

MSE - 트레이닝 데이터: 24.72, 테스트 데이터: 32.35
R2 - 트레이닝 데이터: 0.71, 테스트 데이터: 0.61

Elastic Net 적용

MSE - 트레이닝 데이터: 24.38, 테스트 데이터: 31.87
R2 - 트레이닝 데이터: 0.71, 테스트 데이터: 0.62

리지 회귀, 라쏘 기법에서 인자로 입력되는 alpha의 값을 적절하게 조절하여 회귀 모델의 적합도를 향상 시킬 수 있습니다. 

[23편] '회귀 분석 - 준비하기'에서 회귀 분석에는 단순 회귀 분석과 다중 회귀 분석이 있다고 했습니다. 단순 회귀 분석은 설명 변수가 1개인 경우이며, 다중 회귀 분석은 설명 변수가 2개 이상인 경우라고 말했지요.

우리는 [25편]까지 1978년 보스턴 외곽 지역의 14개 범주의 주택 정보 데이터 중 방의 개수(RM)와 주택 가격(MEDV)에 대해서 회귀 모델을 계산했습니다. RM-MEDV 분포는 설명 변수가 1개이므로 단순 회귀 모델로 분석할 수 있으며, 데이터의 분포와 계산된 회귀 모델은 2차원 평면에 표현할 수 있습니다.

만약 설명 변수가 2개인 다중 회귀 분석의 경우, 데이터의 분포와 계산된 회귀 모델은 3차원 공간에 표현할 수 있을 것입니다. 이 때 회귀 모델은 2차원 평면이 되겠지요. 그런데, 설명 변수가 3개 이상인 다중 회귀 분석인 경우에는 이를 시각적으로 표현할 방법이 없습니다.

아무튼 우리는 이런 사실을 염두해 두고 진행하도록 하지요~

우리가 계산한 회귀 모델에 대한 적합도를 확인하는 방법은 대표적으로 다음과 같은 두 가지가 있습니다.

• 잔차 분석(Residual Analysis)
• 결정 계수(Coefficient of determination)

계산한 회귀 모델이 어느 정도의 적합도를 가지고 있는지 계산하려면 전체 데이터에서 일부분은 회귀 모델을 구하기 위한 트레이닝 데이터로 사용하고 나머지 데이터를 이용해 회귀 모델을 테스트하는 것이 여러면에서 좋습니다.

잔차 분석

​

잔차(residual)는 회귀 모델에 의해 예측된 반응 값 y^와 실제 반응 값 y의 차를 말합니다. 결국 이전 포스팅에서 언급한 offset과 동일한 개념입니다.

아래의 코드를 봅니다.

skl_ra.py

skl_ra.py는 보스턴 외곽 지역 주택정보 14개 범주에서 처음 13개는 설명변수로 하고 주택 가격 MEDV는 반응 값으로 하여 잔차를 분석하는 코드입니다.

>>> X = df.iloc[:, :-1].values

주택 정보에서 마지막 열(MEDV)을 제외한 열의 값들을 X로 둡니다.

>>> X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3,

                                                              random_state=0)

데이터의 70%는 트레이닝 데이터로, 나머지 30%는 테스트 데이터로 하기 위해 데이터를 분리합니다.

나머지 코드는 matplotlib을 이용해 가로축은 회귀 모델에 의해 예측된 값, 세로축은 잔차로 하는 좌표 평면에서 트레이닝 데이터의 예측값 vs. 잔차, 테스트 데이터의 예측값 vs. 잔차를 각각 파란색 동그라미, 연두색 사각형으로 표시하고, 잔차가 0이 되는 기준선을 빨간색 선으로 표시합니다.

코드를 실행하면 다음과 같은 결과가 나옵니다.

위 그림과 같은 그래프를 잔차 그림(Residual Plot)이라 부릅니다. 회귀 모델의 적합도는 예측값에 대한 잔차가 0에 가까울수록 좋습니다. 잔차 그림에서 잔차 0 기준선으로부터 멀리 떨어진 데이터는 이상치로 분류할 수 있을 것입니다.

결정 계수 R2

통계학에서 추정한 예측 모델이 주어진 자료에 적합도를 표현하는 척도로 결정 계수라는 것을 사용합니다. 결정 계수는 R 제곱으로 표현하며 0과 1사이의 값을 가집니다. 결정 계수는 다음과 같이 정의됩니다.

여기서, y(i)와 y^(i)는 각각 i번째 데이터의 반응값과 예측 반응값이며, μy는 반응값의 평균입니다. 이 수식은 뭔가 익숙한 수식으로 구성되어 있습니다. 위 수식에서 분수식의 분자는 회귀 모델을 구하기 위해 사용된 식에서 봤으며, 분모는 반응값 y의 분산입니다.

위 식의 분자는 평균 제곱 오차(Mean Square Error: MSE)로 불리는 식입니다.

MSE만으로도 회귀 모델의 적합도를 정량적으로 나타내는 하나의 척도로 사용할 수 있습니다. MSE의 값이 0에 가까울 수록 적합도가 높은 것입니다.

만약 트레이닝 데이터에 대한 MSE와 테스트 데이터에 대한 MSE를 비교해서, 테스트 데이터에 대한 MSE의 값이 다소 크게 나온다면 계산한 예측 모델이 오버피팅 되었다고 볼 수 있습니다. 따라서 트레이닝 데이터의 MSE와 테스트 데이터의 MSE가 엇비슷한 수준인 경우가 바람직합니다.

자, 다시 결정 계수는 아래와 같은 식으로 정의할 수 있습니다.

여기서 Var(y)는 y의 분산입니다. 앞서 말한 바와 같이 결정 계수는 0과 1사이의 값을 가지며 1에 가까울 수록 적합도가 높다는 것을 의미합니다.

아래의 코드를  skl_ra.py의 맨 아래에 추가합니다.

​

​

​

이 코드는 위 잔차 그림에 해당하는 데이터들에 대한 MSE와 결정 계수의 값을 계산하여 화면에 출력하는 코드입니다.

코드를 실행한 결과는 아래와 같습니다.

MSE - 트레이닝 데이터: 19.96, 테스트 데이터: 27.20

R2 - 트레이닝 데이터: 0.76, 테스트 데이터: 0.67

MSE의 값을 보면, 테스트 데이터의 MSE가 트레이닝 데이터의 MSE에 비해 크게 나옵니다. 즉 이는 우리가 계산한 회귀 모델이 오버피팅 되어있음을 의미합니다. 결정 계수의 값을 보더라도 트레이닝 데이터의 값에 비해 테스트 데이터에 대한 결정 계수값이 다소 작게 나옵니다.

​

​이제 skl_ra.py에서 lr = Regression()을 찾아 아래의 코드로 수정하여 RANSAC 알고리즘을 적용한 회귀 모델에 대해 MSE와 결정 계수를 계산해봅니다.

​

​

​

위 코드로 수정한 skl_ra.py를 실행하여 나온 MSE와 결정 계수의 값은 아래와 같습니다.

​

MSE - 트레이닝 데이터: 23.52, 테스트 데이터: 33.67

R2 - 트레이닝 데이터: 0.72, 테스트 데이터: 0.60

​

​

결과를 보면 RANSAC을 적용한 회귀 모델의 적합도가 RANSAC을 적용하지 않은 회귀 모델의 적합도보다 더 나쁘게 나온다는 것을 알 수 있습니다. MSE의 값은 커졌고 오버피팅 결과로 나오며 결정 계수의 값도 더 낮게 나옵니다.

​

물론 RANSAC의 residual_threshold의 값을 적절하게 조절하면 더 나은 결과를 보일 수도 있습니다.​

아무튼 이번에는 RANSAC을 적용하지 않는 회귀 모델이 조금 더 나은 결과를 보인다는 것을 알 수 있네요.​

​

회귀 모델에 대한 적합도를 측정하는 방법은 이 정도에서 마무리 하도록 하겠습니다.

회귀 모델은 이상치(outlier)라 불리는 주류 또는 정상 분포에서 벗어난 값에 의해 영향을 많이 받습니다. 데이터 과학자들은 이런 이상치들을 그들의 경험과 산업 분야에 대한 지식에 근거해 걸러냅니다.

RANSAC(RANdom SAample Consensus)이라 불리는 알고리즘은 정상 분포에 속해 있는 데이터 집합(이를 inlier로 부릅니다)으로 회귀 분석을 수행할 수 있게 해주는 기법입니다.

RANSAC 알고리즘은 다음과 같은 절차로 수행됩니다.

1. 데이터에서 임의의 개수를 선택하여 이를 inlier로 가정하고 회귀 모델을 구합니다.
2. 나머지 데이터들을 회귀 모델과 비교하고 사용자가 지정한 허용 오차내에 있는 데이터들을 inlier로 포함시킵니다.
3. 재구성된 inlier를 이용해 다시 회귀 모델을 구합니다.
4. 회귀 모델과 inlier의 오차를 측정합니다.
5. 이 오차가 사용자가 지정한 값 내에 있거나 지정한 알고리즘 구동 반복회수에 도달했으면 종료합니다. 만약 이 조건을 만족하지 못하면 1단계부터 다시 시작합니다.

scikit-learn은 RANSAC 알고리즘을 위한 RANSACRegressor 객체를 제공합니다. 아래의 코드를 봅니다.

skl_ransac.py

[24편]의 skl_lrgd.py와 달라진 부분은 LinearRegression()을 RANSACRegressor() 객체의 첫 번째 인자로 대입한 부분입니다.

>>> ransac = RANSACRegressor(LinearRegression(), max_trials=100, min_samples=50,

                            residual_metric=lambda x: np.sum(np.abs(x), axis=1),

                            residual_threshold=5.0, random_state=0)

RANSACRegressor의 인자는 다음과 같은 의미를 가집니다.

• max_trials: 알고리즘의 최대 반복 회수
• min_samples: inlier 값으로 무작위로 선택할 샘플의 최소 개수
• residual_metric: 회귀 모델과 데이터의 오차 측정 함수 지정
• residual_threshold: inlier로 포함시키기 위한 허용 오차

residual_metric에 지정된 람다 함수는 샘플 데이터와 회귀 모델과의 수직 거리의 합을 계산하는 것입니다.

residual_threshold의 값으로 5.0을 지정하여 허용 오차가 5.0 이내이면 inlier로 포함시킵니다. 이 값을 지정하지 않으면 scikit-learn은 허용 오차 값으로 대상 변수 y의 중앙값 절대 편차(Median Absolute Deviation)를 디폴트로 지정합니다. RANSAC에서 이 허용 오차의 값을 적절하게 지정하는 것은 중요한데, 적절한 허용 오차를 찾는 것이 또 다른 문제가 되기도 합니다. 이는 데이터를 분석하는 사람의 경험치나 능력으로 해결되는 문제입니다. 아무튼 여기서는 허용 오차의 값을 5.0으로 지정했습니다.

나머지 코드는 inlier와 특이값을 산점도로 그리고, 회귀 모델을 matplotlib으로 그려주는 로직입니다. skl_ransac.py를 실행하면 아래와 같은 결과가 나옵니다.

위 그림에서 파란색 원으로 표시된 데이터가 inlier이며 연두색 사각형으로 표시된 데이터가 이상치입니다. skl_ransac.py를 실행하여 도출된 회귀선 기울기와 절편의 값을 이전 포스팅의 skl_lrgd.py를 실행하여 도출된 값과 비교해보면 기울기는 9.102에서 9.621로 변했고, y절편의 값도 -34.671에서 -37.137로 변했다는 것을 알 수 있습니다.

이상치를 포함한 모든 데이터에 대해서 계산한 회귀 모델과 이상치를 제거한 후 계산한 회귀 모델 중 어느 것이 더 더 나은 것인지는 테스트를 하기 전까지는 알기 어렵습니다. 다음 포스팅에서는 우리가 계산한 회귀 모델의 적합도에 대해 정량적으로 측정하고 분석하는 방법에 대해 살펴보겠습니다.

[23편]에서 다룬 1978년 미국 보스턴 외곽 지역의 주택 정보 중 몇가지 특성에 대한 히트맵을 다시 불러오겠습니다.

위 히트맵에서 방의 개수(RM)와 주택가격(MEDV)의 상관관계를 보면 피어슨 상관계수의 값이 0.7이므로 매우 강한 양의 상관관계를 가지고 있다는 것을 알 수 있습니다. 이는 방의 개수가 많으면 주택가격이 비싸지는 경향이 있다는 것이지요.

이번 포스팅에서는 RM-MEDV의 데이터 분포에 가장 일치하는 회귀직선을 구하는 것을 파이썬으로 구현해봅니다.

데이터 분포와 가장 일치하는 회귀 모델을 구하는 방법 중 하나가 최소제곱법(Ordinary Least Square; OLS)을 이용하는 것인데, 회귀 모델에 의해 예측되는 반응값 y^와 실제 반응값 y와 차의 제곱의 합이 최소가 되는 회귀 모델을 구하는 것입니다. 이는 곧 바로 앞 포스팅에서 언급한 오프셋의 제곱의 합이 최소가 되는 직선을 구하는 것과 같습니다.

[23편]에서 회귀 모델을 아래와 같이 정의했지요.

​ 

오프셋은 다음과 같이 정의했습니다.

최소제곱법은 모든 데이터에 대해 오프셋을 제곱하고 모두 더한 값이 최소가 되는 것이므로 아래의 값이 최소가 되는 회귀모델을 구하는 것입니다. (데이터의 개수를 n개라 가정합니다.) 

앗,, 이 수식 어디선가 본듯합니다. 바로 아래의 아달라인 비용함수 J(w)와 비슷합니다.

앞에 곱해진 1/2을 무시하면 위의 두 식은 그냥 똑같습니다. 기억이 가물가물하다면, 아래의 링크를 살포시 눌러서 아달라인에 대해 복습을 하고 옵니다.

☞ 아달라인 복습하러 가기

아달라인은 비용함수 J(w)의 값이 최소가 되도록 순입력 함수의 가중치를 업데이트 한다고 했습니다.

그런데,  회귀 모델을 구하는 것도 결국 J(w)의 값이 최소가 되는 회귀 모델의 y절편과 설명변수 x의 계수인 w0, w1을 구하는 것이므로 아달라인을 구현한 코드를 그대로 가져와서 조금만 수정하면 될 것 같습니다.

아래의 코드를 봅니다.

lrgd0.py

이 코드는 [7편]에 있는 아달라인을 구현한 adaline.py에서 predict(self,X)의 리턴값만 바꾼겁니다. 아래의 링크를 눌러서 adaline.py 코드를 보고옵니다

☞ 아달라인 구현 코드 보러 가기

최소제곱법 기반 회귀 모델의 가중치를 구하는 LinearRegressionGD()는 아달라인의 활성화 함수의 결과값을 -1 또는 1로 변환하는 것만 빼고는 동일한 로직임을 알 수 있습니다.

lrgd0.py 코드의 아랫부분에 아래 코드를 추가합니다.

lrgd1.py 

이 코드는 RM-MEDV의 표준화된 값을 이용하여, 비용함수의 가중치를 업데이트 하는 반복회수를 x축에, LinearRegressionGD에 의해 계산되는 비용함수의 값을 y축에 두고 그래프를 그립니다. 실행 결과는 다음과 같습니다.

그래프를 보면 5회 계산에서 값이 수렴함을 알 수 있습니다. 즉 이 부분에서 회귀 모델이 정해지는 겁니다.

아래 코드를 lrgd1.py 코드 아랫부분에 추가합니다.

lrgd2.py

이 코드는 표준화 된 RM값을 x축에, 표준화 된 MEDV값을 y축으로 해서 RM-MEDV의 분포를 나타내고 위에서 구한 회귀 모델을 그립니다. 코드를 실행하면 아래와 같은 결과가 나옵니다.

회귀 모델을 구했으므로 방이 5개인 주택 가격을 예측해 보도록 하겠습니다. 이 그래프는 표준화된 값으로 되어 있습니다. 따라서 실제 집값으로 환산하려면 표준화된 값을 원래 값으로 변환해 주어야겠지요. 아래의 코드를 lrgd2.py 코드에 추가합니다.

lrgd3.py 

num_rooms는 RM의 값을 지정해주는 곳입니다. 방이 5개인 주택가격을 알아보고자 하는 것이므로 실수형으로 5.0을 대입합니다. 우리가 구한 회귀 모델은 표준화 값에 기반하므로, 방의 개수 5.0을 표준화되 값으로 변환한 후 회귀 모델에 의한 예측값을 구해야 합니다. 이 예측값 역시 표준화된 값이며, 표준화된 값을 원래의 값으로 변환시켜주는 것은 StandardScaler.inverse_transform()을 이용하면 됩니다.

코드를 실행하면 아래와 같은 결과가 나옵니다.

방이 [5]개인 주택가격은 약 [10840]달러입니다.

scikit-learn을 이용하여 회귀 모델 구하기

​

이 포스팅에서 여태까지 다룬 내용은 최소제곱법 기반으로 회귀직선을 구하는 원리와 구현 코드를 작성해보는 것이었습니다. 그런데, 이 내용을 이해했다면 앞으로 scikit-learn이 제공해주는 API를 이용하는 것이 더 낫습니다.  

scikit-learn의 회귀 분석 API를 사용하면 표준화시키고 표준화시킨 값을 본래값으로 변환시키고 하는 번거로운 작업을 해줄 필요가 없습니다. 이런 번거로운 작업들은 scikit-learn 회귀 분석 API 내부적으로 다 처리해주기 때문이죠. 

아래의 코드를 봅니다.

skl_lrgd.py 

이 코드는 scikit-learn의 LinearRegression()을 이용해 RM-MEDV의 회귀 모델 기울기와 y절편을 구하고, RM-MEDV의 분포와 회귀 모델을 그래프로 그립니다. 데이터를 분석할 때 회귀 모델의 기울기나 y절편의 값이 중요한 의미를 가질때 가 있는데, 이럴 경우 위 코드를 참조하여 회귀 모델의 기울기나 y절편을 구하면 됩니다.

코드를 실행하면 다음과 같은 결과가 화면에 나옵니다.

이제 아래의 코드를 skl_lrgd.py 코드 아랫부분에 추가하고 실행하면 앞에서 예측한 방 5개짜리 주택가격과 동일한 결과가 나오는 것을 볼 수 있습니다.

우리가 여태까지 다루었던 퍼셉트론, 로지스틱 회귀, SVM, 의사결정 트리, 랜덤 포레스트, kNN과 같은 알고리즘은 트레이닝 데이터를 학습한 후, 주어진 데이터에 대해 어떤 그룹에 속하는지 또는 어떤 범주에 포함되는지 예측하는 분류를 위한 알고리즘입니다.

이번 포스팅에서 다룰 회귀 분석(Regression Analysis)은 분류가 아니라 데이터들 사이의 상관관계라던가, 추이를 예측한다던가, 대상 값 자체를 예측하는 지도학습 알고리즘입니다. 예를 들어, 방의 개수와 집값의 상관 관계라던가, 과거 10년간의 영업 실적을 분석하여 미래의 영업 실적을 예측하는 것 등은 회귀 분석으로 가능합니다.

아래의 식을 살포시 봅니다.

이 식은 우리가 잘 알고 있는 1차 함수이며, 입력 값이 1개인 퍼셉트론의 순입력 함수로 볼 수 있습니다. 회귀 분석에서는 x를 설명 변수(explanatory variable)라 부르고, y^를 반응 변수(response variable) 또는 대상 변수(target variable)라 부릅니다. 그리고 가중치 w0은 y절편,  w1은 설명 변수의 계수가 됩니다.

회귀 분석은 주어진 데이터 (x, y)의 분포를 분석하여 이 분포와 가장 일치하는 직선을 구하는 것이 최종 목표입니다. 결국 회귀 분석의 최종 목표는 데이터 (x, y)의 분포와 가장 일치하는 직선이 되는 w0와 w1을 계산하는 것입니다.