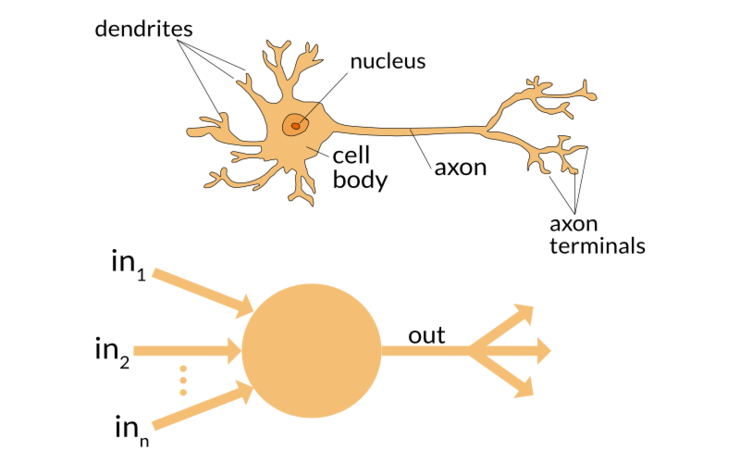
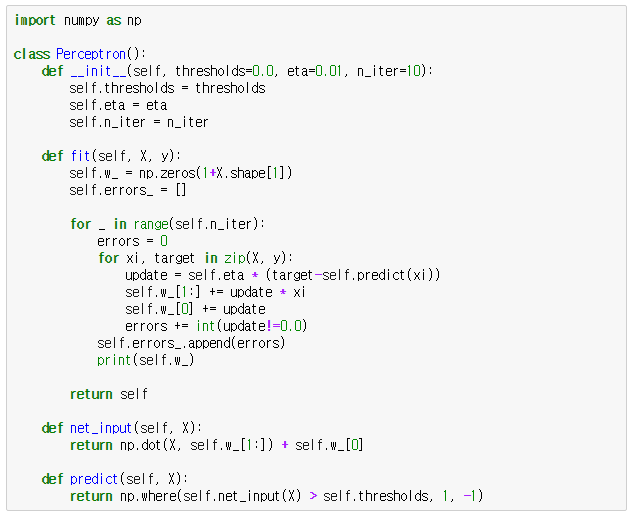
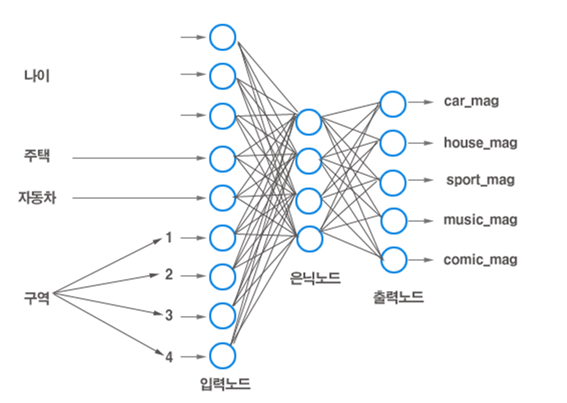
Chapter3. 사이킷런을 사용한 머신러닝 분류기.
사이킷런을 이용한 퍼셉트론 훈련.
from sklearn import datasets
import numpy as np
iris = datasets.load_iris()
#print(iris)
X = iris.data[:, [2, 3]] # petal length, petal width
y = iris.target
print('Class labels: ', np.unique(y))
# 훈련용과 테스트용으로 분리
from sklearn.cross_validation import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=0)
from sklearn.preprocessing import StandardScaler
sc = StandardScaler()
sc.fit(X_train)
X_train_std = sc.transform(X_train)
X_test_std = sc.transform(X_test)
from sklearn.linear_model import Perceptron
ppn = Perceptron(max_iter=40, eta0=0.1, random_state=0)
ppn.fit(X_train_std, y_train)
y_pred = ppn.predict(X_test_std)
print('y_pred: ', y_pred)
print('y_test: ', y_test)
print('Misclassified samples : %d' % (y_test != y_pred).sum()) # 4 / 45(test_data) = 0.089
# 테스트 데이터에 대한 퍼셉트론의 분류 정확도
from sklearn.metrics import accuracy_score
print('Accuracy: %.2f' % accuracy_score(y_test, y_pred)) # y_test : 진분류, y_pred : 예측 분류
# 테스트 데이터로부터의 샘플인 것을 강조하기 위해 테스트 데이터에는 작은 원을 더하도록 변경.
from matplotlib.colors import ListedColormap
import matplotlib.pyplot as plt
def plot_decision_regions(X, y, classifier, test_idx=None, resolution=0.02):
markers = ('s', 'x', 'o', '^', 'v')
colors = ('red', 'blue', 'lightgreen', 'gray', 'cyan')
cmap = ListedColormap(colors[:len(np.unique(y))])
# plot the decision surface
x1_min, x1_max = X[:, 0].min() - 1, X[:, 0].max() + 1
x2_min, x2_max = X[:, 1].min() - 1, X[:, 1].max() + 1
xx1, xx2 = np.meshgrid(np.arange(x1_min, x1_max, resolution), np.arange(x2_min, x2_max, resolution))
Z = classifier.predict(np.array([xx1.ravel(), xx2.ravel()]).T)
Z = Z.reshape(xx1.shape)
plt.contourf(xx1, xx2, Z, alpha=0.4, cmap=cmap)
plt.xlim(xx1.min(), xx1.max())
plt.ylim(xx2.min(), xx2.max())
#plot all samples
X_test, y_test = X[test_idx, :], y[test_idx]
for idx, cl in enumerate(np.unique(y)):
plt.scatter(x=X[y == cl, 0], y=X[y == cl, 1], alpha=0.8, c=cmap(idx), marker=markers[idx], label=cl)
if test_idx:
X_test, y_test = X[test_idx, :], y[test_idx]
plt.scatter(X_test[:, 0], X_test[:, 1], c='', alpha=1.0, linewidth=1, marker='o', s=55, label='test set')
X_combined_std = np.vstack((X_train_std, X_test_std))
y_combined = np.hstack((y_train, y_test))
#print('X_combined_std: ', X_combined_std)
#print('y_combined: ', y_combined)
plot_decision_regions(X=X_combined_std, y=y_combined, classifier=ppn, test_idx=range(105,150))
plt.xlabel('petal length [standardized]')
plt.ylabel('petal width [standardized]')
plt.legend(loc='upper left')
plt.show()
# 시그모이드
import matplotlib.pyplot as plt
import numpy as np
def sigmoid(z):
return 1.0 / (1.0 + np.exp(-z))
z = np.arange(-7, 7, 0.1)
#print('z: ', z)
phi_z = sigmoid(z)
#print('phi_z: ', phi_z)
plt.plot(z, phi_z)
plt.axvline(0.0, color='k') # x축 중앙선
plt.axhspan(0.0, 1.0, facecolor='1.0', alpha=1.0, ls='dotted')
plt.axhline(y=0.5, ls='dotted', color='k') # y축 중앙선
plt.yticks([0.0, 0.5, 1.0])
plt.ylim(-0.1, 1.1)
plt.xlabel('z')
plt.ylabel('$\phi (z)$')
plt.show()
# 사이킷런으로 로지스틱 회귀 모델 훈련하기
from sklearn.linear_model import LogisticRegression
lr = LogisticRegression(C=1000.0, random_state=0)
lr.fit(X_train_std, y_train)
plot_decision_regions(X_combined_std, y_combined, classifier=lr, test_idx=range(105,150))
plt.xlabel('petal length [standardized]')
plt.ylabel('petal width [standardized]')
plt.legend(loc='upper left')
plt.show()
'''오버피팅(overfitting) - 훈련 데이터에 대한 모델의 성능은 좋으나 경험하지 못한 데이터(테스트 데이터)에
대해서는 잘 일반화되지 못하는 것.
'''
# 역정규화 파라미터 C에 대해 여러 가지 값을 갖는 10개의 로지스틱 회귀 모델을 피팅했다.
# 파라미터 C를 감소시키면(즉, 정규화 강도를 증가시키면) 가중계수는 수축한다.
weights, params = [], []
for c in np.arange(-5, 5):
lr = LogisticRegression(C=10**np.float32(c), random_state=0)
lr.fit(X_train_std, y_train)
weights.append(lr.coef_[1])
params.append(10**np.float32(c))
weights = np.array(weights)
plt.plot(params, weights[:, 0], label='petal length')
plt.plot(params, weights[:, 1], label='petal width', linestyle='--')
plt.ylabel('weight coefficient')
plt.xlabel('C')
plt.legend(loc='upper left')
plt.xscale('log')
plt.show()
# 서포트 벡터 머신의 마진 분류 최대화
# SVM 모델 훈련
from sklearn.svm import SVC
svm = SVC(kernel='linear', C=1.0, random_state=0)
svm.fit(X_train_std, y_train)
plot_decision_regions(X_combined_std, y_combined, classifier=svm, test_idx=range(105, 150))
plt.xlabel('petal length [standardized]')
plt.ylabel('petal width [standardized]')
plt.legend(loc='upper left')
plt.show()
# 퍼셉트론, 로지스틱 회귀, 서포트 벡터 머신의 확률적 그래디언트 디센트 버전을 초기 설정
from sklearn.linear_model import SGDClassifier
ppn = SGDClassifier(loss='perceptron')
lr = SGDClassifier(loss='log')
svm = SGDClassifier(loss='hinge')
np.random.seed(0)
X_xor = np.random.randn(200, 2)
#print('X_xor: ', X_xor)
y_xor = np.logical_xor(X_xor[:, 0] > 0, X_xor[:, 1] > 0)
#print('y_xor: ', y_xor)
y_xor = np.where(y_xor, 1, -1)
#print('X_xor[y_xor==1, 0]: ', X_xor[y_xor==1, 0])
#print('X_xor[y_xor==1, 1]: ', X_xor[y_xor==1, 1])
plt.scatter(X_xor[y_xor==1, 0], X_xor[y_xor==1, 1], c='b', marker='x', label='1')
plt.scatter(X_xor[y_xor==-1, 0], X_xor[y_xor==-1, 1], c='r', marker='s', label='-1')
plt.ylim(-3.0)
plt.legend()
plt.show()
svm = SVC(kernel='rbf', random_state=0, gamma=0.10, C=10.0)
svm.fit(X_xor, y_xor)
plot_decision_regions(X_xor, y_xor, classifier=svm)
plt.legend(loc='upper left')
plt.show()
svm = SVC(kernel='rbf', random_state=0, gamma=0.2, C=1.0)
svm.fit(X_train_std, y_train)
plot_decision_regions(X_combined_std, y_combined, classifier=svm, test_idx=range(105, 150))
plt.xlabel('petal length [standardized]')
plt.ylabel('petal width [standardized]')
plt.legend(loc='upper left')
plt.show()
svm = SVC(kernel='rbf', random_state=0, gamma=100.0, C=1.0)
svm.fit(X_train_std, y_train)
plot_decision_regions(X_combined_std, y_combined, classifier=svm, test_idx=range(105, 150))
plt.xlabel('petal length [standardized]')
plt.ylabel('petal width [standardized]')
plt.legend(loc='upper left')
plt.show()
# 의사결정나무 학습
import matplotlib.pyplot as plt
import numpy as np
def gini(p):
return (p)*(1 - (p)) + (1 - p)*(1 - (1-p))
def entropy(p):
return - p*np.log2(p) - (1 - p)*np.log2((1 - p))
def error(p):
return 1 - np.max([p, 1 - p])
x = np.arange(0.0, 1.0, 0.01)
ent = [entropy(p) if p != 0 else None for p in x]
sc_ent = [e*0.5 if e else None for e in ent]
err = [error(i) for i in x]
fig = plt.figure()
ax = plt.subplot(111)
for i, lab, ls, c, in zip([ent, sc_ent, gini(x), err],
['Entropy', 'Entropy (scaled)', 'Gini Impurity', 'Misclassification Error'],
['-', '-', '--', '-.'],
['black', 'lightgray', 'red', 'green', 'cyan']):
line = ax.plot(x, i, label=lab, linestyle=ls, lw=2, color=c)
ax.legend(loc='upper center', bbox_to_anchor=(0.5, 1.15), ncol=3, fancybox=True, shadow=False)
ax.axhline(y=0.5, linewidth=1, color='k', linestyle='--')
ax.axhline(y=1.0, linewidth=1, color='k', linestyle='--')
plt.ylim([0, 1.1])
plt.xlabel('p(i=1)')
plt.ylabel('Impurity Index')
plt.show()
# 의사결정나무 만들기
from sklearn.tree import DecisionTreeClassifier
tree = DecisionTreeClassifier(criterion='entropy', max_depth=3, random_state=0)
tree.fit(X_train, y_train)
X_combined = np.vstack((X_train, X_test))
y_combined = np.hstack((y_train, y_test))
print('X_train: ', X_train)
print('y_train: ', y_train)
plot_decision_regions(X_combined, y_combined, classifier=tree, test_idx=range(105, 150))
plt.xlabel('petal length [cm]')
plt.ylabel('petal width [cm]')
plt.legend(loc='upper left')
plt.show()
from sklearn.tree import export_graphviz
export_graphviz(tree, out_file='tree.dot', feature_names=['petal length', 'petal width'])
from sklearn.ensemble import RandomForestClassifier
forest = RandomForestClassifier(criterion='entropy', n_estimators=10, random_state=1, n_jobs=2)
forest.fit(X_train, y_train)
plot_decision_regions(X_combined, y_combined, classifier=forest, test_idx=range(105,150))
plt.xlabel('petal length')
plt.ylabel('petal width')
plt.legend(loc='upper left')
plt.show()
# 유클리디안(Euclidean) 거리 메트릭을 사용하여 사이킷런에서 KNN 모델 구현
from sklearn.neighbors import KNeighborsClassifier
knn = KNeighborsClassifier(n_neighbors=5, p=2, metric='minkowski')
knn.fit(X_train_std, y_train)
plot_decision_regions(X_combined_std, y_combined, classifier=knn, test_idx=range(105,150))
plt.xlabel('petal length [standardized]')
plt.ylabel('petal width [standardized]')
plt.show()